



suivant: Table des matières
monter: math
précédent: 7.8.0.2 Position des plans
Table des matières
- 1. La force
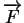 s'exerce en
s'exerce en  .
.
- . La règle du parallélogramme.
- 3. La composition des forces est associative.
- . La multiplication par
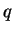 altère l'intensité et le sens de
altère l'intensité et le sens de
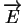 .
.
- 1. On choisit
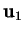 ,
, 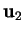 , ... dans
, ... dans 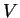 tant que c'est possible.
tant que c'est possible.
- 2. Les plans vectoriels contenant une droite vectorielle.
- 1. Pour composer des translations, on additionne leurs vecteurs.
- 2. La translation de vecteur
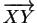 est la seule transformant
est la seule transformant  en
en 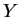 .
.
- . La relation de Chasles: trois points déterminent au plus deux directions indépendantes.
- 4. L'espace affine
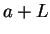 .
.
- .
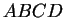 est un parallélogramme car
est un parallélogramme car 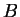 et
et 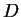 sont les images de
sont les images de  et
et 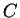 par une même translation.
par une même translation.
- . Dans
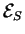 , l'addition résulte de la règle du parallélogramme.
, l'addition résulte de la règle du parallélogramme.
- . La ``droite réelle" comme modèle des droites.
- 8. Le rapport de section.
- . Le barycentre de
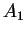 , ... ,
, ... , 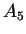 est calculé progressivement en remplaçant
est calculé progressivement en remplaçant 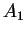 et
et 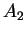 par leur barycentre
par leur barycentre 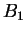 ,
, 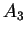 et
et 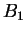 par le leur,... A chaque étape, les poids sont ajustés.
par le leur,... A chaque étape, les poids sont ajustés.
- . La droite
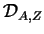 passe par le milieu de
passe par le milieu de
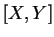 qui est aussi celui de
qui est aussi celui de
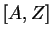
- . Une droite caractérisée par un point et un vecteur directeur.
- . Dans un plan, deux droites qui ne sont pas parallèles sont sécantes...
- . La porte ouverte
 coupe le mur
coupe le mur 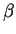 selon la droite qui traverse les charnières...
selon la droite qui traverse les charnières...
- . Une droite non parallèle à un plan le perce en un seul point...
- . Les droites
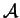 et
et
 sont gauches.
sont gauches.
- .
 et
et 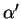 ne sont pas parallèles:
ne sont pas parallèles:
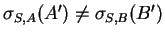 .
.
- . Quand
 et
et 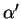 sont parallèles,
sont parallèles,
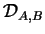 et
et
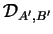 le sont aussi.
le sont aussi.
- . Le théorème de Menelaüs.
- . Si
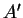 ,
, 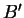 et
et 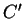 sont alignés, les droites
sont alignés, les droites 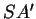 ,
, 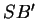 et
et 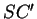 sont coplanaires.
sont coplanaires.
- . Le théorème de Ceva, lorsque les droites se coupent...
- 21. ...et quand elles ne se coupent pas.
- . Repères, axes et simplexes en dimensions
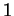 ,
, 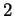 et
et 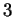 .
.
- . Axes et projections parallèles.
- . Le théorème de Desargues.
- . Angle non orienté.
- . La tête à l'envers...
- . Angles orientés (sens trigonométrique).
- . Le champ magnétique incurve la trajectoire de la partiucule (
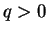 ).
).
- . Les solutions de l'équation
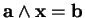 .
.
- 1. Angle de deux droites.
- 2. Angle d'une droite et d'un hyperplan.
- 3. Angle de deux hyperplans.
- 4.
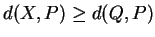 .
.
- 5.
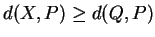 .
.
- 6. Distance de deux droites gauches...
- 7.
 est la projection orthogonale de
est la projection orthogonale de  sur
sur 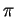 .
.
- . Angle et côté d'un triangle sphérique...
- . La distance de
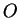 à
à
 est
est
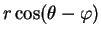 .
.
- . Coordonnées sphériques.
- .
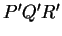 est l'image de
est l'image de 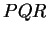 par l'homothétie de centre
par l'homothétie de centre 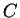 et de rapport
et de rapport 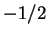 .
.
- . Symétrie centrale
- .
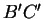 est l'image de
est l'image de 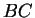 par l'homothétie
par l'homothétie
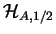 .
.
- .
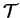 est linéaire entre les espaces de vecteurs liés en des points se correspondant.
est linéaire entre les espaces de vecteurs liés en des points se correspondant.
- . Un sommet d'un parallélogramme est combinaison affine des autres.
- . Symétrie et projections.
- . Réflexion...
- 8. Rotation plane d'angle
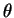 et centre
et centre 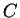 .
.
- . L'angle d'une rotation spatiale n'est pas univoquement déterminé.
- . La dérivée de
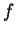 est un vecteur.
est un vecteur.
- . Trajectoire d'un point matériel.
- . Hélice circulaire droite.
- 4. Le folium de Descartes.
- . Développement de Taylor en
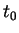 .
.
- 6. Rayon de courbure et courbure.
- . La concavité est orientée dans le sens de la normale principale.
- . Le trièdre de Frenet.
- . Discontinuité de la normale principale quand
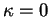 .
.
- . Coniques définies par foyer et directrice.
- 11. Promenade le long d'une hyperbole...
- . Paramétrage par des coordonnées.
- . Paramétrage quelconque.
- .
 engendre un paraboloïde hyperbolique.
engendre un paraboloïde hyperbolique.
- .
 est la projection stéréographique de
est la projection stéréographique de  .
.
- . Changement de paramétrages dans l'hémisphère sud.
- 6. Surface.
- 7. Courbes et vecteurs tangents sur
 .
.
- .
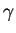 est composé de
est composé de 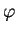 et de d'une courbe dans
et de d'une courbe dans 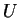 .
.
- . Plan tangent à
 .
.
- 10. Un ruban de Moebius.
- 11. Cylindre circulaire droit.
- . Dériver
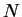 dans la direction de
dans la direction de 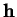 : application de Weingarten.
: application de Weingarten.
- .
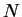 et
et 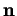 font un angle calculé grâce au théorème de Meusnier.
font un angle calculé grâce au théorème de Meusnier.
- . Deux courbes tracées sur
 et tangentes à
et tangentes à 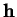 .
.
- . Signe de
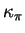 et concavité de la section par un plan normal
et concavité de la section par un plan normal 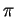 .
.
- 16. E,
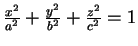 .
.
- 17. H1,
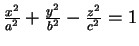 .
.
- 18. H1, d'un autre point de vue.
- 19. H2,
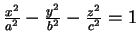 .
.
- 20. PE,
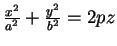 .
.
- 21. PH,
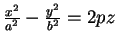 .
.
- . En s'éloignant le long d'une génératrice, le plan tangent tend vers une position limite à laquelle il est orthogonal au point central de
la génératrice.
- . La position du plan tangent le long de la génératrice est déterminée par la distance au point central.
2002-12-17