



suivant: 6.4.3.2 Classification des courbes
monter: 6.4.3.1 Les coniques proprement
précédent: 6.4.3.1 Les coniques proprement
Table des matières
Conservons les notations de la démonstration précédente. On va à présent écrire l'équation polaire du lieu décrit dans la proposition ci-dessus en prenant
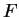 comme origine et
comme origine et 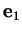 comme vecteur de référence du système de coordonnées polaires. La distance à
comme vecteur de référence du système de coordonnées polaires. La distance à
 d'un point
d'un point  de coordonnées polaires
de coordonnées polaires
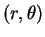 vaut
vaut
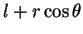 . Celle de
. Celle de  à
à 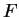 valant
valant 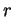 , il vient donc, pour un point du lieu,
ou encore
, il vient donc, pour un point du lieu,
ou encore
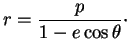 |
|
|
(6.7) |
Quand 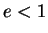 , le dénominateur de cette fraction est toujours positif. L'angle
, le dénominateur de cette fraction est toujours positif. L'angle 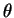 varie donc librement dans
varie donc librement dans 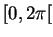 et y décrit toute l'ellipse.
et y décrit toute l'ellipse.
Quand 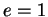 ,
le dénominateur est positif sauf en
,
le dénominateur est positif sauf en 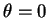 pour lequel il s'annule. Ceci correspond au fait que l'axe polaire
pour lequel il s'annule. Ceci correspond au fait que l'axe polaire
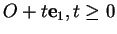 est sur l'axe de symétrie de la
parabole et orienté à l'opposé du sommet par rapport au foyer, qui est obtenu en
est sur l'axe de symétrie de la
parabole et orienté à l'opposé du sommet par rapport au foyer, qui est obtenu en
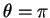 .
.
Figure 11:
Promenade le long d'une hyperbole...
|
|
Quand 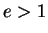 ,
, 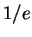 est le cosinus d'un angle
est le cosinus d'un angle
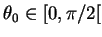 .
Lorsque
.
Lorsque 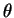 varie dans
varie dans
![$ ]\theta_0,2\pi-\theta_0[$](img1996.gif) ,
, 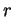 est positif et l'équation ci-dessus décrit la branche de l'hyperbole relative au foyer
est positif et l'équation ci-dessus décrit la branche de l'hyperbole relative au foyer 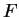 . Par contre,
lorsque
. Par contre,
lorsque
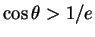 , c'est l'autre branche qui est décrite: de 0 à
, c'est l'autre branche qui est décrite: de 0 à 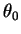 , on en parcourt la moitié inférieure(6.12), en s'éloignant du sommet; de
, on en parcourt la moitié inférieure(6.12), en s'éloignant du sommet; de
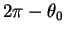 à 0,
on en décrit l'autre moitié en se rapprochant du sommet, le point
à 0,
on en décrit l'autre moitié en se rapprochant du sommet, le point  étant d'autant plus éloigné de celui-ci que
étant d'autant plus éloigné de celui-ci que 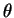 est proche de
est proche de 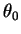 .
L'angle
.
L'angle 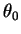 est l'angle non orienté que fait chaque asymptote avec l'axe focal.
est l'angle non orienté que fait chaque asymptote avec l'axe focal.
Lorsque 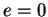 , l'équation (29) représente une circonférence, de centre
, l'équation (29) représente une circonférence, de centre  et de rayon
et de rayon 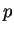 , à condition d'oublier que
, à condition d'oublier que 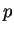 est initialement défini
comme le produit de la distance
est initialement défini
comme le produit de la distance
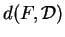 par l'excentricité et de supposer que c'est un nombre positif donné.
par l'excentricité et de supposer que c'est un nombre positif donné.




suivant: 6.4.3.2 Classification des courbes
monter: 6.4.3.1 Les coniques proprement
précédent: 6.4.3.1 Les coniques proprement
Table des matières
2002-12-17
![]() , le dénominateur de cette fraction est toujours positif. L'angle
, le dénominateur de cette fraction est toujours positif. L'angle ![]() varie donc librement dans
varie donc librement dans ![]() et y décrit toute l'ellipse.
et y décrit toute l'ellipse.
![]() ,
le dénominateur est positif sauf en
,
le dénominateur est positif sauf en ![]() pour lequel il s'annule. Ceci correspond au fait que l'axe polaire
pour lequel il s'annule. Ceci correspond au fait que l'axe polaire
![]() est sur l'axe de symétrie de la
parabole et orienté à l'opposé du sommet par rapport au foyer, qui est obtenu en
est sur l'axe de symétrie de la
parabole et orienté à l'opposé du sommet par rapport au foyer, qui est obtenu en
![]() .
.
![]() , l'équation (29) représente une circonférence, de centre
, l'équation (29) représente une circonférence, de centre ![]() et de rayon
et de rayon ![]() , à condition d'oublier que
, à condition d'oublier que ![]() est initialement défini
comme le produit de la distance
est initialement défini
comme le produit de la distance
![]() par l'excentricité et de supposer que c'est un nombre positif donné.
par l'excentricité et de supposer que c'est un nombre positif donné.