Soient un arc paramétré de courbe ![]() et un de ses paramétrage
et un de ses paramétrage
![]() .
Le développement de Taylor en
.
Le développement de Taylor en ![]()
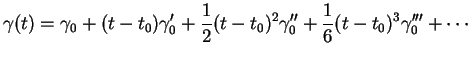
de ![]() (l'indice 0 signale que les fonctions sont évaluées en
(l'indice 0 signale que les fonctions sont évaluées en ![]() ) fournit différentes approximations de
) fournit différentes approximations de ![]() , aux ordres
, aux ordres ![]() ,
, ![]() , etc.
A l'ordre
, etc.
A l'ordre ![]() , par exemple,
, par exemple, ![]() est confondu avec sa tangente en
est confondu avec sa tangente en ![]() . A l'ordre deux, il est approché par une courbe du second degré située dans un
plan passant par
. A l'ordre deux, il est approché par une courbe du second degré située dans un
plan passant par ![]() et parallèle à
et parallèle à ![]() et
et
![]() .
En général, les vecteurs
.
En général, les vecteurs ![]() ,
,
![]() et
et
![]() sont linéairement indépendants (6.5) et
fournissent une base de
sont linéairement indépendants (6.5) et
fournissent une base de
![]() .
.
L'idée du trièdre de Frenet est d'exploiter cette base (rendue orthonormée) dans le cas d'un paramétrage naturel afin de décoder l'information géométrique contenue dans ces approximations.