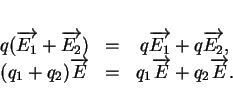suivant: Géométrie
monter: Chapitre Introduction
précédent: Modèle et abstraction
Table des matières
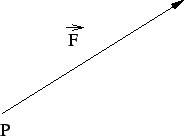
On va illustrer ce qui précède à propos du calcul vectoriel. Une force non nulle
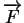 est caractérisée non seulement par une intensité mais aussi par une
direction et un sens.
est caractérisée non seulement par une intensité mais aussi par une
direction et un sens.
Figure 1:
La force
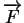 s'exerce en
s'exerce en  .
.
|
|
Par conséquent, elle est généralement décrite par un segment orienté dont la longueur est proportionnelle à l'intensité de la force et dont l'origine est éventuellement le point sur lequel elle s'exerce. La loi de composition des forces est donnée par la "règle du parallélogramme". A priori, elle n'a pas grand chose à voir avec l'addition numérique. Pourtant, il est commode de noter
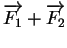 la résultante de force s'exerçant en un même point.
la résultante de force s'exerçant en un même point.
Figure:
La règle du parallélogramme.
|
|
Ceci est légitimé par le fait que cette "addition"
partage beaucoup de propriétés avec celle des nombres. Par exemple, elle est commutative, ce qui signifie que l'on a toujours
et associative, ce qui signifie que l'ordre selon lequel on groupe plus de deux forces pour les composer est indifférent:
Figure 3:
La composition des forces est associative.
|
|
On sait, par une des lois de Coulomb, que la force
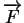 exercée par une distribution de charges électriques sur une charge ponctuelle
exercée par une distribution de charges électriques sur une charge ponctuelle 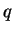 placée en un point
placée en un point  est proportionnelle à
est proportionnelle à 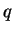 . Ceci s'écrit
. Ceci s'écrit
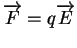 , où
, où
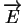 est le champ électrique en
est le champ électrique en  . Dans le produit
. Dans le produit
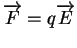 , le rôle de
, le rôle de 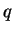 n'est pas banal. Non seulement il multiplie l'intensité de
n'est pas banal. Non seulement il multiplie l'intensité de
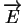 par
par 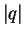 mais il en affecte le sens qui change ou non selon que
mais il en affecte le sens qui change ou non selon que 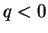 ou
ou 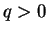 . Pourtant, la notation multiplicative est assez appropriée car cette opération a des propriétés formellement semblables à celles du produit de nombres.
Par exemple, elle est distributive par rapport à l'addition:
. Pourtant, la notation multiplicative est assez appropriée car cette opération a des propriétés formellement semblables à celles du produit de nombres.
Par exemple, elle est distributive par rapport à l'addition:
Figure:
La multiplication par 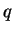 altère l'intensité et le sens de
altère l'intensité et le sens de
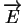 .
.
|
|
Faisant abstraction de la signification physique des symboles
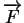 ,
,
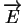 ,
, 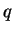 , ... nous voyons émerger une structure dans laquelle on peut
additionner des objets, les multiplier par des nombres, ces deux opérations vérifiant des règles de calculs avec lesquelles nous nous sommes familiarisés
depuis les bancs de l'école primaire.
, ... nous voyons émerger une structure dans laquelle on peut
additionner des objets, les multiplier par des nombres, ces deux opérations vérifiant des règles de calculs avec lesquelles nous nous sommes familiarisés
depuis les bancs de l'école primaire.
Cette structure mathématique est celle d'espace vectoriel et l'algèbre associée s'appelle le calcul vectoriel. Ces notions sont d'une très grande
utilité en physique mais aussi en mathématique, singulièrement en géométrie.




suivant: Géométrie
monter: Chapitre Introduction
précédent: Modèle et abstraction
Table des matières
2002-12-17