2.8.2 Formulation classique

On obtient des versions plus classiques du théorème de Desargues en sectionnant les six droites de l'énoncé par un plan $\alpha$ ne passant pas par leur point commun. Les droites ${\mathcal A}_i$ et ${\mathcal A}_i'$ percent $\alpha$ selon deux triangles $A_1A_2A_3$ et $A_1'A_2'A_3'$ respectivement. Les plans ${\mathcal A}_1{\mathcal A}_1'$, ${\mathcal A}_2{\mathcal A}_2'$ et ${\mathcal A}_3{\mathcal A}_3'$ coupent $\alpha$ selon les droites $A_1A_1'$, $A_2A_2'$ et $A_3A_3'$ joignant les sommets homologues de ces triangles. Le fait que les plans ${\mathcal A}_1{\mathcal A}_1'$, ${\mathcal A}_2{\mathcal A}_2'$ et ${\mathcal A}_3{\mathcal A}_3'$ possèdent une droite commune ${\mathcal D}$ se traduit par le fait que les droites $A_1A_1'$, $A_2A_2'$ et $A_3A_3'$ se coupent ou sont parallèles selon que ${\mathcal D}$ perce $\alpha$ ou lui est parallèle. Chacune des droites ${\mathcal A}_1{\mathcal A}_2\cap{\mathcal A}_1'{\mathcal A}_2'$, ${\mathcal A}_2{\mathcal A}_3\cap{\mathcal A}_2'{\mathcal A}_3'$ et ${\mathcal A}_3{\mathcal A}_1\cap{\mathcal A}_3'{\mathcal A}_1'$ perce le plan $\alpha$ ou lui est parallèle. Le fait qu'elle soient coplanaires se traduit donc par l'une des situations suivantes que l'on distingue par le nombre d'intersections non vides parmi $A_1A_2\cap A_1'A_2'$, $A_2A_3\cap A_2'A_3'$ et $A_3A_1\cap A_3'A_1'$:

• {Trois intersections non vides} Les droites prolongeant les cotés homologues des triangles $A_1A_2A_3$ et $A_1'A_2'A_3'$ se coupent deux à deux selon des points alignés.
• {Deux intersections non vides} Deux paires de droites prolongeant les côtés homologues des triangles $A_1A_2A_3$ et $A_1'A_2'A_3'$ se coupent en des points situés sur une parallèle aux côtés homologues restants.
• {Trois intersections vides} Les côtés homologues des triangles $A_1A_2A_3$ et $A_1'A_2'A_3'$ sont parallèles deux à deux.

Il serait fastidieux d'avoir à tenir compte de tous ces cas possibles. Voici un des énoncés que l'on peut déduire du Théorème 8.1. Il permet entre autre, à l'aide d'une règle seulement, de tracer une droite passant par un point donné et par l'intersection de deux droites données se coupant hors de l'épure.

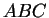
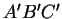
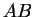
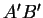
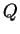
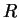
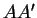
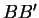
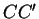
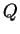
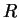
Théorème 2.8.2   (Théorème de Desargues) Soient deux triangles $ABC$ et $A'B'C'$ d'un plan dont les sommets sont deux à deux distincts et dont les prolongements des paires de côtés homologues $AB$, $A'B'$, etc. se coupent en des points $P$, $Q$, $R$. Les droites $AA'$, $BB'$, $CC'$ sont sécantes ou parallèles si et seulement si les points $P$, $Q$ et $R$ sont alignés.

Figure: Le théorème de Desargues.