



suivant: 7.3.0.1 Exemples
monter: 7 Surfaces
précédent: 7.2.0.3 Paramétrages équivalents
Table des matières
En éliminant les paramètres 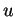 et
et 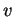 des composantes
des composantes 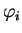 d'un paramétrage
d'un paramétrage
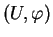 , on arrive parfois à exprimer la condition nécessaire et suffisante pour qu'un point
, on arrive parfois à exprimer la condition nécessaire et suffisante pour qu'un point  de
de
 appartienne à la portion régulière de surface
appartienne à la portion régulière de surface
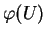 sous la forme d'une équation
sous la forme d'une équation 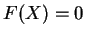 .
Celle-ci n'est éventuellement définie que dans une partie de
.
Celle-ci n'est éventuellement définie que dans une partie de
 , le plus
souvent un ouvert
, le plus
souvent un ouvert 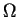 . On démontre de plus en analyse qu'il est possible de faire en sorte que
. On démontre de plus en analyse qu'il est possible de faire en sorte que
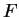 soit de classe
soit de classe 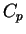 dans
dans 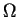 et que son gradient ne s'y
annule pas.
et que son gradient ne s'y
annule pas.
Inversement, si
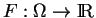 est de classe
est de classe 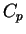 et si
et si
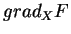 ne s'annule en aucun point de
ne s'annule en aucun point de 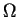 , alors l'ensemble
des zéros de
, alors l'ensemble
des zéros de 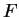 est Ñ localement Ñ une portion régulière de surface.
Plus précisément, si la dérivée partielle de
est Ñ localement Ñ une portion régulière de surface.
Plus précisément, si la dérivée partielle de 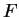 par rapport à une
des coordonnées n'est pas nulle en un point, il peut être
paramétré par les deux autres au voisinage de ce point. En outre, les
paramétrages de
par rapport à une
des coordonnées n'est pas nulle en un point, il peut être
paramétré par les deux autres au voisinage de ce point. En outre, les
paramétrages de
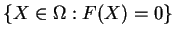 sont toujours équivalents
dans les ouverts correspondants aux points qu'ils décrivent
simultanément.
sont toujours équivalents
dans les ouverts correspondants aux points qu'ils décrivent
simultanément.
Nous dirons que
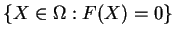 est une surface et que
est une surface et que
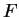 en est une équation cartésienne dans
en est une équation cartésienne dans 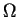 (7.1).
(7.1).
Sous-sections




suivant: 7.3.0.1 Exemples
monter: 7 Surfaces
précédent: 7.2.0.3 Paramétrages équivalents
Table des matières
2002-12-17
![]() est de classe
est de classe ![]() et si
et si
![]() ne s'annule en aucun point de
ne s'annule en aucun point de ![]() , alors l'ensemble
des zéros de
, alors l'ensemble
des zéros de ![]() est Ñ localement Ñ une portion régulière de surface.
Plus précisément, si la dérivée partielle de
est Ñ localement Ñ une portion régulière de surface.
Plus précisément, si la dérivée partielle de ![]() par rapport à une
des coordonnées n'est pas nulle en un point, il peut être
paramétré par les deux autres au voisinage de ce point. En outre, les
paramétrages de
par rapport à une
des coordonnées n'est pas nulle en un point, il peut être
paramétré par les deux autres au voisinage de ce point. En outre, les
paramétrages de
![]() sont toujours équivalents
dans les ouverts correspondants aux points qu'ils décrivent
simultanément.
sont toujours équivalents
dans les ouverts correspondants aux points qu'ils décrivent
simultanément.