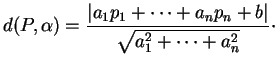suivant: 4.4.2.2 Distance d'un point
monter: 4.4.2 Distance entre variétés
précédent: 4.4.2 Distance entre variétés
Table des matières
Soient un point  et un hyperplan
et un hyperplan  déterminé par un de ses points
déterminé par un de ses points  et une de ses normales
et une de ses normales 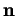 .
Supposons
.
Supposons  extérieur à
extérieur à  .
L'idée pour calculer la distance
.
L'idée pour calculer la distance
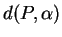 entre
entre  et
et  est de choisir un point
est de choisir un point 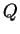 de
de  pour que la droite
pour que la droite 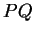 lui soit perpendiculaire.
Pour tout
lui soit perpendiculaire.
Pour tout
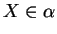 , le triangle
, le triangle 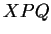 étant alors rectangle en
étant alors rectangle en 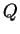 , on a en effet
si bien que
, on a en effet
si bien que
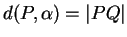 . Le point cherché est nécessairement de la forme
. Le point cherché est nécessairement de la forme
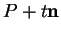 , où
, où 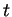 est choisi pour que
Il y a donc un seul point répondant à la question et
formule qui convient évidemment aussi lorsque
est choisi pour que
Il y a donc un seul point répondant à la question et
formule qui convient évidemment aussi lorsque  est un point de
est un point de  .
.
Le point 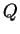 en lequel la distance entre
en lequel la distance entre  et
et  est réalisée s'appelle la projection orthogonale de
est réalisée s'appelle la projection orthogonale de  sur
sur  (c'est donc
(c'est donc  si celui-ci
appartient à
si celui-ci
appartient à  ). On la note
). On la note
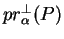 .
Quand l'hyperplan est donné par une équation cartésienne
.
Quand l'hyperplan est donné par une équation cartésienne
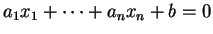 dans un repère orthonormé dans lequel les cordonnées de
dans un repère orthonormé dans lequel les cordonnées de  sont
sont
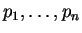 , l'expression ci-dessus prend une forme particulièrement simple
, l'expression ci-dessus prend une forme particulièrement simple
En effet, on peut prendre pour 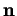 le vecteur de composantes
le vecteur de composantes
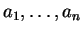 et si
et si
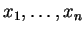 sont les coordonnées de
sont les coordonnées de  , on a
, on a
Figure 4:
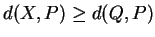 .
.
|
|




suivant: 4.4.2.2 Distance d'un point
monter: 4.4.2 Distance entre variétés
précédent: 4.4.2 Distance entre variétés
Table des matières
2002-12-17
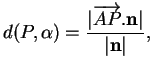
![]() en lequel la distance entre
en lequel la distance entre ![]() et
et ![]() est réalisée s'appelle la projection orthogonale de
est réalisée s'appelle la projection orthogonale de ![]() sur
sur ![]() (c'est donc
(c'est donc ![]() si celui-ci
appartient à
si celui-ci
appartient à ![]() ). On la note
). On la note
![]() .
Quand l'hyperplan est donné par une équation cartésienne
.
Quand l'hyperplan est donné par une équation cartésienne
![]() dans un repère orthonormé dans lequel les cordonnées de
dans un repère orthonormé dans lequel les cordonnées de ![]() sont
sont
![]() , l'expression ci-dessus prend une forme particulièrement simple
, l'expression ci-dessus prend une forme particulièrement simple