suivant: 6.3 Arcs réguliers de
monter: 6.2.2 Dérivée des fonctions
précédent: 6.2.2 Dérivée des fonctions
Table des matières
Si 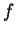 n'a qu'un argument,
n'a qu'un argument, 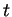 , cela n'a plus beaucoup d'intérêt de le dériver dans une direction
, cela n'a plus beaucoup d'intérêt de le dériver dans une direction
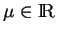 . On utilise plus directement sa dérivée
par rapport à
. On utilise plus directement sa dérivée
par rapport à 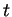 qui est donnée par, si elle existe,
Dans un repère, les composantes de ce vecteur sont les dérivées par rapport à
qui est donnée par, si elle existe,
Dans un repère, les composantes de ce vecteur sont les dérivées par rapport à 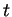 des coordonnées de
des coordonnées de 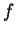 :
:
Figure:
La dérivée de 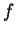 est un vecteur.
est un vecteur.
|
|
Remarque 6.2.5
On adapte facilement ce qui précède pour définir les dérivées de fonctions à valeurs dans ou définies sur un espace vectoriel. Cela permet par exemple de
dériver
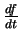
et d'introduire ainsi les dérivées d'ordre supérieur de
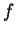
.
Remarque 6.2.6
On étend la notion de fonction dérivable sur un intervalle fermé borné en considérant, aux extrémités de celui-ci, les dérivées à gauche et à droite.
Il est parfois commode de noter 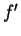 ,
, 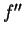 ,
, 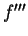 , etc. les dérivées successives de
, etc. les dérivées successives de 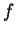 par rapport à
par rapport à 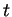 .
.
Proposition 6.2.7
Soient des fonctions
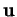
,
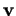
,
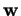
définies sur un intervalle
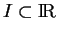
et à valeurs dans un espace vectoriel Euclidien

(de dimension
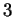
et
orienté le cas échéant). Si elles sont dérivables dans
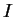
, alors
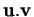
,
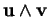
et
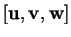
sont dérivables dans
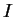
et
De plus, si
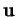
est de longueur constante dans
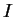
, alors
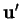
est orthogonal à
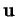
.
Preuve. Les deux premières égalités annoncées résultent immédiatement des expressions du produit scalaire et du produit vectoriel dans une base orthonormée et des
règles de calcul usuelles des dérivées. Pour le produit mixte, il vient alors
Si les
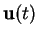 sont tous de même longueur, alors la fonction
sont tous de même longueur, alors la fonction
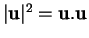 est constante dans
est constante dans 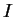 et sa dérivée
est nulle.
et sa dérivée
est nulle.




suivant: 6.3 Arcs réguliers de
monter: 6.2.2 Dérivée des fonctions
précédent: 6.2.2 Dérivée des fonctions
Table des matières
2002-12-17
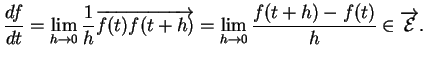
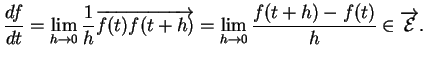
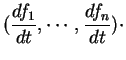
![]() ,
, ![]() ,
, ![]() , etc. les dérivées successives de
, etc. les dérivées successives de ![]() par rapport à
par rapport à ![]() .
.