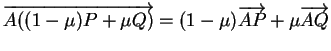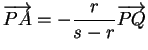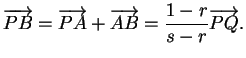suivant: 2.3.3 Mesure des segments
monter: 2.3 Combinaisons affines
précédent: 2.3.1 Combinaisons affines
Table des matières
Etant donné deux nombres 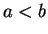 , tout nombre
, tout nombre 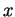 est combinaison affine
est combinaison affine
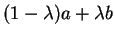 de
de 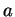 et de
et de 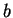 et s'écrit de manière unique sous cette forme.
En effet, comme
et s'écrit de manière unique sous cette forme.
En effet, comme 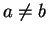 , l'équation
, l'équation
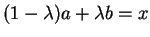 admet
admet
comme seule solution. De plus, 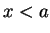 ,
,
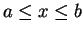 et
et 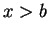 selon que
selon que
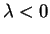 ,
,
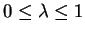 et
et
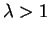 respectivement.
respectivement.
Figure:
La ``droite réelle" comme modèle des droites.
|
|
Par analogie, nous appellerons droite de
 l'ensemble des combinaisons affines de deux points distincts de
l'ensemble des combinaisons affines de deux points distincts de
 . Si
. Si 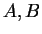 sont distincts, on note
sont distincts, on note
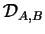 , ou encore
, ou encore 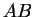 , la droite passant par
, la droite passant par  et
et 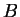 , c'est-à-dire
De plus, nous apellerons segment de droite joignant A et B l'ensemble
, c'est-à-dire
De plus, nous apellerons segment de droite joignant A et B l'ensemble
Proposition 2.3.2
Soient des points distincts
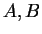
de

.
(i) 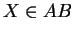 si et seulement si
si et seulement si
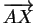 est un multiple de
est un multiple de
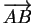 .
.
(ii) Si
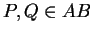 sont distincts, alors
sont distincts, alors 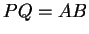 .
.
Preuve. (i) En effet,
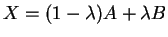 si et seulement si
si et seulement si
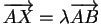 .
.
(ii) Il existe 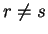 tels que
tels que
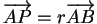 et
et
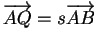 . En particulier,
. En particulier,
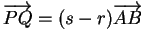 . Cela étant,
. Cela étant,
est un multiple de
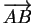 . Par conséquent,
. Par conséquent,
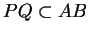 . De plus,
. De plus,
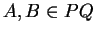 car
et
On a donc aussi
car
et
On a donc aussi
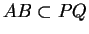 .
.
Vu (ii), deux droites distinctes ont au plus un point en commun. Quand elles en ont un, on dit qu'elles sont sécantes, ou qu'elles se coupent en ce
point.




suivant: 2.3.3 Mesure des segments
monter: 2.3 Combinaisons affines
précédent: 2.3.1 Combinaisons affines
Table des matières
2002-12-17
![]() , tout nombre
, tout nombre ![]() est combinaison affine
est combinaison affine
![]() de
de ![]() et de
et de ![]() et s'écrit de manière unique sous cette forme.
En effet, comme
et s'écrit de manière unique sous cette forme.
En effet, comme ![]() , l'équation
, l'équation
![]() admet
admet
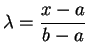
![]() si et seulement si
si et seulement si
![]() est un multiple de
est un multiple de
![]() .
.
![]() sont distincts, alors
sont distincts, alors ![]() .
.![]() tels que
tels que
![]() et
et
![]() . En particulier,
. En particulier,
![]() . Cela étant,
. Cela étant,