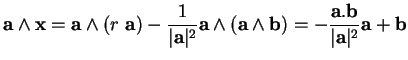suivant: 4
Géométrie Euclidienne
monter: 3.3.3
Orientation en dimension
précédent: 3.3.3.1 Produit mixte Table des matières
La force agissant sur une particule électrique résultant
d'un champ électromagnétique est donnée par
Figure: Le champ
magnétique incurve la trajectoire de la partiucule ( ).
).
|
|
Dans cette expression,  est la charge électrique
de la particule,
est la charge électrique
de la particule,  est la vitesse de la lumière,
est la vitesse de la lumière, 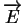 est le champ éléctrique et
est le champ éléctrique et 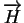 est le champ
magnétique mesurés au point où se trouve la
particule. Celle-ci est en mouvement et la contribution de
est le champ
magnétique mesurés au point où se trouve la
particule. Celle-ci est en mouvement et la contribution de 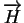 à la force dépend de sa
vitesse
à la force dépend de sa
vitesse 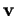 .
Cette
dépendance est relativement compliquée. Elle s'exprime au
moyen d'une nouvelle opération sur les vecteurs, le produit
vectoriel
.
Cette
dépendance est relativement compliquée. Elle s'exprime au
moyen d'une nouvelle opération sur les vecteurs, le produit
vectoriel 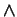 . En voici la définition.
. En voici la définition.
La règle des mineurs appliquée à la
troisième
colonne de (17) montre que
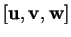 est le produit scalaire de
est le produit scalaire de
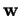 et du vecteur de
composantes
et du vecteur de
composantes
Celui-ci ne dépend donc pas non plus de la base
orthonormée positive utilisée: comme 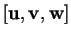 ,
il dépend seulement de l'orientation de
,
il dépend seulement de l'orientation de 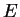 .
On l'appelle produit vectoriel de
.
On l'appelle produit vectoriel de 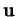 et de
et de 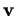 . On le note
. On le note 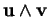 .
Preuve. Les points (i), (ii) et (v) résultent
immédiatement de la définition du produit vectoriel.
.
Preuve. Les points (i), (ii) et (v) résultent
immédiatement de la définition du produit vectoriel.
Il vient,
On en déduit aussitôt (iii). Enfin,
D'où (iv).
Remarque 3.3.6 La propriété (iii)
signifie que la longueur de
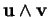
est l'aire
du ``parallélogramme" construit sur
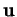
et
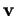
, phrase qui prendra
tout son sens
quand les notions métriques auront été
interprétées en géométrie affine. Dans le
même ordre d'idée, la valeur absolue du produit mixte
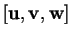
est le volume du ``parallélépipède" construit sur
ses trois arguments.
Revenant à l'expression de la force agissant sur une particule
électrique, on voit par la propriété ci-dessus,
que le champ magnétique contribue à modifier non
seulement l'intensité mais aussi la direction de sa vitesse.
La propriété suivante est immédiate mais utile.
Proposition 3.3.7 Soit une base
positive orthonormée
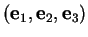
. Si deux des indices
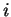
et
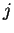
sont
égaux, alors
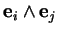
est
nul. Si les indices
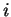
,
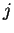
,
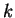
sont deux à deux distincts, alors
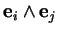
est
égal à
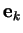
si
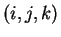
est une permutation circulaire de
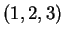
et à
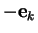
sinon.
Proposition 3.3.8 (Formules du double produit
vectoriel)
Pour tous
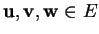
,
on a
Preuve. Démontrons la première formule, la
seconde se vérifiant de façon analogue ou s'en
déduisant par antisymétrie, au choix. On développe
les deux membres selon une
base orthonormée positive 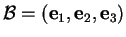 de
de  . En utilisant la linéarité
de la formule par rapport à
. En utilisant la linéarité
de la formule par rapport à 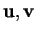 et
et 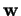 , on
est ramené au cas où ceux-ci sont des
éléments arbitraires de
, on
est ramené au cas où ceux-ci sont des
éléments arbitraires de 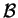 , c'est-à-dire à vérifier
que
pour tous
, c'est-à-dire à vérifier
que
pour tous 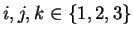 .
Cela donne en principe
.
Cela donne en principe 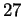 vérifications mais en
réfléchissant un peu, à l'aide de la proposition
précédente, on réduit significativement le travail
nécessaire.
Lorsque
vérifications mais en
réfléchissant un peu, à l'aide de la proposition
précédente, on réduit significativement le travail
nécessaire.
Lorsque 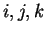 sont tous distincts, les deux
membres de l'égalité proposée sont nuls car
sont tous distincts, les deux
membres de l'égalité proposée sont nuls car 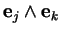 est
alors
est
alors 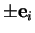 tandis que
tandis que 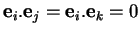 .
Même conclusion lorsque
.
Même conclusion lorsque 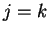 ,
trivialement.
Il reste donc à envisager les cas où
,
trivialement.
Il reste donc à envisager les cas où 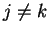 et
et  est égal à
est égal à 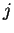 ou à
ou à 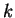 . On peut d'ailleurs se limiter
à
. On peut d'ailleurs se limiter
à 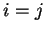 , par antisymétrie en
, par antisymétrie en
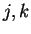 . Ceci laisse finalement six cas:
et ceux où
. Ceci laisse finalement six cas:
et ceux où 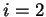 ou
ou 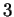 . La
vérification est alors directe. Par exemple pour
. La
vérification est alors directe. Par exemple pour 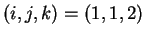 , il vient immédiatement
D'où la propriété.
, il vient immédiatement
D'où la propriété.
Remarque 3.3.9 Il est utile de retenir les formules
en français. Elles se lisent toutes les deux comme ceci:
un double produit vectoriel est égal au vecteur du milieu
multiplié par le produit scalaire des deux autres moins le
produit de l'autre vecteur de la parenthèse
et du produit scalaire des deux autres.
Proposition 3.3.10 Soient
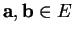
. Si
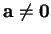
, alors
l'équation
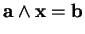 |
(3.4) |
a des solutions si et seulement si
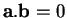
. Lorsque
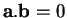
, ses
solutions sont données par
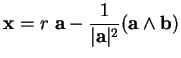 |
(3.5) |
où
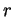
est un nombre arbitraire.
Preuve. En effet, si l'équation proposée admet
une solution, alors en multipliant les deux membres de (18) vectoriellement par 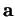 et en
développant le double produit vectoriel, il vient
Donc, en supposant
et en
développant le double produit vectoriel, il vient
Donc, en supposant 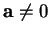 ,
est de la forme (19).
,
est de la forme (19).
Inversement, si 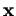 est donné par (19), alors
est donné par (19), alors
et 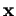 est
une solution de (18) si et seulement si
est
une solution de (18) si et seulement si 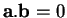 (car
(car 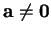 ).
).
Figure: Les solutions de
l'équation 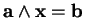 .
.
|
|




suivant: 4
Géométrie Euclidienne
monter: 3.3.3
Orientation en dimension
précédent: 3.3.3.1 Produit mixte Table des matières
2002-12-17
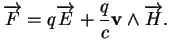
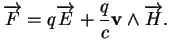
![]() est le produit scalaire de
est le produit scalaire de
![]() et du vecteur de
composantes
et du vecteur de
composantes
![]() ,
où
,
où ![]() est l'angle non orienté
formé par
est l'angle non orienté
formé par ![]() et
et ![]() . En particulier,
. En particulier, ![]() si
et seulement si
si
et seulement si
![]() et
et ![]() sont
linéairement dépendants.
sont
linéairement dépendants.
![]() et
et ![]() sont
linéairement indépendants, alors
sont
linéairement indépendants, alors ![]() est une base positive de
est une base positive de ![]() .
.
![]() .
En particulier,
.
En particulier, ![]() est
orthogonal à
est
orthogonal à ![]() et à
et à ![]() .
.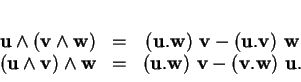
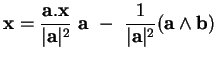
![]() est donné par (19), alors
est donné par (19), alors