



suivant: 1.5.4 Equations cartésiennes
monter: 1.5 Sous-espaces vectoriels
précédent: 1.5.2 Exemples
Table des matières
Un lemme aisé va nous permettre de montrer que tous les sous-espaces vectoriels de 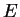 ont des équations paramétriques.
ont des équations paramétriques.
Lemme 1.5.7
Si
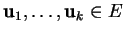
sont tels que
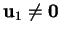
et
alors ils sont linéairement indépendants.
Preuve. On procède par récurrence sur 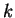 . Pour
. Pour 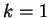 ,
, 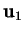 est linéairement indépendant car il n'est pas nul. Passons de
est linéairement indépendant car il n'est pas nul. Passons de 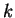 à
à 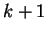 .
Supposons que
Si
.
Supposons que
Si
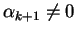 , alors
Donc
, alors
Donc
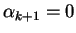 et il reste
En appliquant l'hypothèse de récurrence, on en déduit que les autres
et il reste
En appliquant l'hypothèse de récurrence, on en déduit que les autres 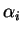 sont nuls .
sont nuls .
Figure 1:
On choisit 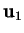 ,
, 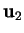 , ... dans
, ... dans 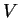 tant que c'est possible.
tant que c'est possible.
|
|
Preuve. (i) On construit de proche en proche des vecteurs
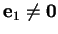 ,
,
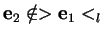 , ... ,
, ... ,
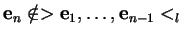 tant que c'est possible, en choisissant les premiers dans
tant que c'est possible, en choisissant les premiers dans 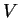 .
A cause du lemme ci-dessus, ils sont linéairement indépendants. Vu le Théorème 4.2, il y en a au plus
.
A cause du lemme ci-dessus, ils sont linéairement indépendants. Vu le Théorème 4.2, il y en a au plus 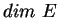 .
En fait, il y en a exactement
.
En fait, il y en a exactement 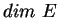 car s'il y en avait moins, alors
et l'on pourrait en choisir un de plus. Donc
car s'il y en avait moins, alors
et l'on pourrait en choisir un de plus. Donc
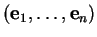 est une base de
est une base de 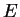 .
Semblablement, si
.
Semblablement, si 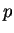 est le numéro du dernier
est le numéro du dernier 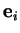 que l'on a pu choisir dans
que l'on a pu choisir dans 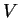 , alors
(éventuellement,
, alors
(éventuellement, 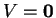 et alors
et alors 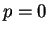 , par convention).
Par conséquent, la dimension de
, par convention).
Par conséquent, la dimension de 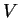 est
est 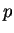 et
et 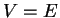 si et seulement si
si et seulement si 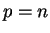 .
.
(ii) Si
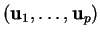 est une base de
est une base de 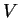 , alors, dans la construction (i) ci-dessus, on peut prendre
, alors, dans la construction (i) ci-dessus, on peut prendre
car, en effet, dans une base, aucun élément n'est combinaison linéaire des autres (Proposition 4.1).
Soient un sous-espace vectoriel 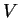 de
de 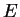 et une base
et une base
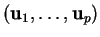 de
de 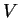 .
Les éléments de
.
Les éléments de 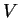 sont donc exactement les
sont donc exactement les
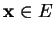 de la forme
de la forme
Cette relation est une équation paramétrique (vectorielle) de 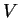 . Le fait que les
. Le fait que les 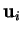 sont linéairement indépendants garantit l'unicité des paramètres
sont linéairement indépendants garantit l'unicité des paramètres
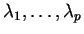 décrivant
décrivant 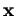 .
.
Exprimée à l'aide des composantes
de 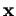 et des
et des 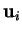 dans une base
dans une base
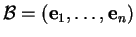 de
de 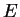 , l'équation paramétrique vectorielle de
, l'équation paramétrique vectorielle de 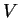 considérée se
traduit par
considérée se
traduit par
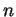 équations paramétriques ``scalaires":
équations paramétriques ``scalaires":
Dans un espace vectoriel de dimension 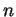 , les sous-espaces vectoriels de dimension
, les sous-espaces vectoriels de dimension 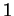 ,
, 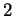 et
et 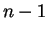 s'appellent droites,
plans et hyperplans vectoriels respectivement.
s'appellent droites,
plans et hyperplans vectoriels respectivement.
Une droite vectorielle est donc l'ensemble des multiples
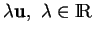 , d'un quelconque de ses éléments non nul
, d'un quelconque de ses éléments non nul
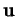 et un plan vectoriel est l'ensemble des combinaisons
et un plan vectoriel est l'ensemble des combinaisons
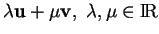 , de deux de ses éléments
, de deux de ses éléments
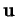 et
et 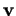 dont aucun n'est multiple de l'autre.
dont aucun n'est multiple de l'autre.




suivant: 1.5.4 Equations cartésiennes
monter: 1.5 Sous-espaces vectoriels
précédent: 1.5.2 Exemples
Table des matières
2002-12-17
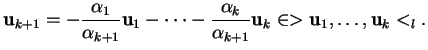
![]() est de dimension finie,
est de dimension finie,
![]() et
et ![]() si et seulement si
si et seulement si
![]() .
.
![]() est contenue dans une base de
est contenue dans une base de ![]() .
.![]() est une base de
est une base de ![]() , alors, dans la construction (i) ci-dessus, on peut prendre
, alors, dans la construction (i) ci-dessus, on peut prendre
![]() de
de ![]() et une base
et une base
![]() de
de ![]() .
Les éléments de
.
Les éléments de ![]() sont donc exactement les
sont donc exactement les
![]() de la forme
de la forme
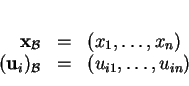
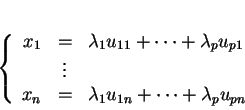
![]() , les sous-espaces vectoriels de dimension
, les sous-espaces vectoriels de dimension ![]() ,
, ![]() et
et ![]() s'appellent droites,
plans et hyperplans vectoriels respectivement.
s'appellent droites,
plans et hyperplans vectoriels respectivement.
![]() , d'un quelconque de ses éléments non nul
, d'un quelconque de ses éléments non nul
![]() et un plan vectoriel est l'ensemble des combinaisons
et un plan vectoriel est l'ensemble des combinaisons
![]() , de deux de ses éléments
, de deux de ses éléments
![]() et
et ![]() dont aucun n'est multiple de l'autre.
dont aucun n'est multiple de l'autre.