



suivant: 5.3 Isométries
monter: 5.2 Applications affines
précédent: 5.2.1 Définition
Table des matières
Voici une caractérisation intéressante des applications affines. On note 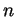 la dimension de
la dimension de
 .
.
Proposition 5.2.5
Soient une application
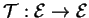
et un repère
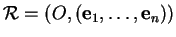
de

et
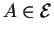
. Les propositions suivantes sont équivalentes.
(i) L'application
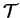 est affine.
est affine.
(ii) Il existe une unique application linéaire
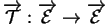 telle que
telle que
pour tous
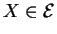
.
(iii) L'application
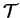 est représentée dans le repère
est représentée dans le repère
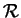 par
par
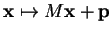 |
(5.1) |
où
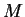
est une matrice carrée de dimension
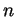
et
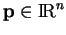
.
De plus, quand
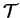 est affine, l'application
est affine, l'application
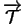 ne dépend pas de
ne dépend pas de  .
.
Figure:
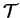 est linéaire entre les espaces de vecteurs liés en des points se correspondant.
est linéaire entre les espaces de vecteurs liés en des points se correspondant.
|
|
Preuve. (i) entraîne (ii). Supposons que
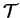 soit affine. Il existe au plus une application
soit affine. Il existe au plus une application
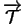 ayant la propriété demandée car celle-ci exige de
poser, pour tout
ayant la propriété demandée car celle-ci exige de
poser, pour tout
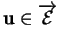 ,
,
Nous allons vérifier que cette définition ne
dépend pas du choix de  et qu'elle donne une application linéaire. Pour prouver l'indépendance par rapport au choix de
et qu'elle donne une application linéaire. Pour prouver l'indépendance par rapport au choix de  , notons que,
, notons que, 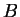 étant un point
quelconque,
étant un point
quelconque, 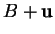 est la combinaison affine
de
est la combinaison affine
de  ,
, 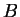 et
et 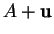 .
.
Figure:
Un sommet d'un parallélogramme est combinaison affine des autres.
|
|
Par conséquent
ce qui s'écrit aussi
Vérifions ensuite que
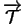 est linéaire. Soient
est linéaire. Soient
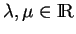 et
et
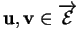 . Le point
. Le point
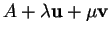 est la combinaison affine
de
est la combinaison affine
de  ,
, 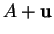 et
et 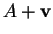 . Par suite,
égalité qu'on peut relire en
. Par suite,
égalité qu'on peut relire en
(ii) entraîne (iii). Dans la base
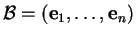 de
de
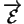 , l'application linéaire
, l'application linéaire
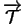 est représentée par une matrice carrée
est représentée par une matrice carrée
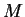 de dimension
de dimension 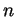 , c'est-à-dire que les composantes de
, c'est-à-dire que les composantes de
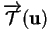 s'obtiennent en appliquant
s'obtiennent en appliquant 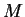 à celles de
à celles de 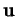 :
:
Si 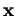 et
et 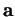 sont les coordonnées respectives de
sont les coordonnées respectives de  et de
et de  dans le repère
dans le repère
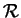 , alors les composantes de
, alors les composantes de
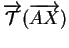 sont donc
sont donc
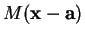 . Dès lors, en notant
. Dès lors, en notant 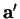 la coordonnée de
la coordonnée de
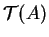 , celle de
, celle de
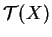 s'écrit
à condition de poser
s'écrit
à condition de poser
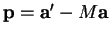 .
.
(iii) entraîne (i). C'est évident.
La proposition précedente stipule qu'une application affine
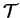 est caractérisée par l'image
est caractérisée par l'image
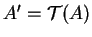 d'un point
d'un point  et par une application
linéaire entre les espaces de vecteurs liés
et par une application
linéaire entre les espaces de vecteurs liés
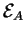 et
et
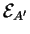 , qui est de plus indépendante du point
, qui est de plus indépendante du point  .
.
Lorsque
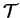 est une translation ou une homothéthie de rapport
est une translation ou une homothéthie de rapport 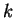 ,
,
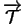 est
est
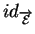 ou
ou
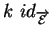 respectivement.
respectivement.
On voit facilement que si
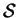 et
et
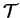 sont des apllications affines, alors
sont des apllications affines, alors
Remarque 5.2.6
Il est utile de retenir que, dans (iii), la matrice
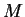
est celle qui représente
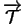
dans la base
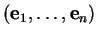
de
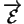
. Pour rappel, la colonne de numéro
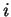
de
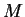
est formée des composantes de
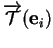
.
Exemple 5.2.7
Les symétries
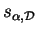
Soient un hyperplan  et une droite
et une droite
 non parallèle à
non parallèle à  . Le symétrique de
. Le symétrique de
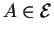 par rapport à
par rapport à  parallèlement à
parallèlement à
 est l'unique point
est l'unique point
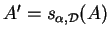 formant avec
formant avec  un segment parallèle à
un segment parallèle à
 et dont le milieu appartient à
et dont le milieu appartient à  .
L'application
.
L'application
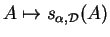 est une affinité. En effet, dans un repère
est une affinité. En effet, dans un repère
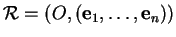 où
où 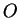 est le point de
percée de
est le point de
percée de
 dans
dans  , où
, où
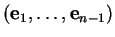 est une base de
est une base de
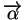 et
et 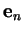 est un vecteur-directeur de
est un vecteur-directeur de
 , elle est représentée
sous la forme (21) avec
, elle est représentée
sous la forme (21) avec
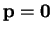 et
et
Exemple 5.2.8
Les projections parallèles
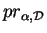
et
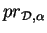
(
5.2)
Figure:
Symétrie et projections.
|
|
Soient encore un hyperplan  et une droite
et une droite
 non parallèle à
non parallèle à  . La projection de
. La projection de
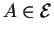 sur
sur  parallèlement à
parallèlement à
 est le
point de percée
est le
point de percée
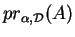 dans
dans  de la droite passant par
de la droite passant par  et parallèle à
et parallèle à
 (5.3). L'application
(5.3). L'application
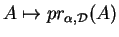 est
affine car, dans un repère comme dans l'exemple précédent, elle est représentée sous la forme (21) avec
est
affine car, dans un repère comme dans l'exemple précédent, elle est représentée sous la forme (21) avec
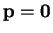 et
et
Semblablement, l'application qui transforme  en sa projection sur
en sa projection sur
 parallèlement à
parallèlement à  , point de percée
, point de percée
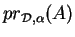 de
de
 dans l'hyperplan plan parallèle à
dans l'hyperplan plan parallèle à  passant par
passant par  , est affine. On a encore
, est affine. On a encore
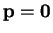 tandis que
tandis que
Remarque 5.2.9
Si les applications affines
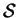
et
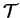
sont représentées dans un repère
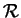
par les applications
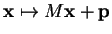 |
|
|
(5.2) |
et
respectivement, alors la composée
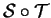
l'est par
Ceci montre que
transforme la composition des applications de la forme (
22) en le produit de matrices(
5.4).
Proposition 5.2.10
Soient un simplexe
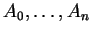
et des points
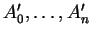
de

.
Il existe une seule application affine
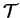
de

qui, pour chaque
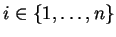
, transforme
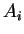
en
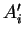
.
C'est une affinité si et seulement si
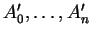
forment également un simplexe.
Preuve. Puisque
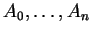 forment un simplexe,
forment un simplexe,
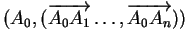 est un repère de
est un repère de
 .
L'application affine représentée dans celui-ci sous la forme (22) en prenant pour
.
L'application affine représentée dans celui-ci sous la forme (22) en prenant pour 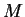 la matrice dont les colonnes sont les composantes de
la matrice dont les colonnes sont les composantes de
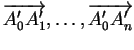 et pour
et pour 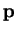 la coordonnée de
la coordonnée de 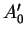 , transforme évidemment chaque
, transforme évidemment chaque 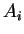 en son homologue
en son homologue 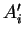 . C'est clairement la
seule application affine ayant cette propriété. C'est une affinité à condition
que la matrice
. C'est clairement la
seule application affine ayant cette propriété. C'est une affinité à condition
que la matrice 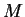 soit non singulière, c'est-à-dire que
soit non singulière, c'est-à-dire que
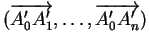 soit une base. Ceci équivaut au fait que
soit une base. Ceci équivaut au fait que
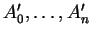 forment un simplexe.
forment un simplexe.




suivant: 5.3 Isométries
monter: 5.2 Applications affines
précédent: 5.2.1 Définition
Table des matières
2002-12-17
![]() la dimension de
la dimension de
![]() .
.
![]() est affine.
est affine.
![]() telle que
telle que
![]() est représentée dans le repère
est représentée dans le repère
![]() par
par
![]() est affine, l'application
est affine, l'application
![]() ne dépend pas de
ne dépend pas de ![]() .
.![]() soit affine. Il existe au plus une application
soit affine. Il existe au plus une application
![]() ayant la propriété demandée car celle-ci exige de
poser, pour tout
ayant la propriété demandée car celle-ci exige de
poser, pour tout
![]() ,
,
![]() de
de
![]() , l'application linéaire
, l'application linéaire
![]() est représentée par une matrice carrée
est représentée par une matrice carrée
![]() de dimension
de dimension ![]() , c'est-à-dire que les composantes de
, c'est-à-dire que les composantes de
![]() s'obtiennent en appliquant
s'obtiennent en appliquant ![]() à celles de
à celles de ![]() :
:
![]()
![]() est caractérisée par l'image
est caractérisée par l'image
![]() d'un point
d'un point ![]() et par une application
linéaire entre les espaces de vecteurs liés
et par une application
linéaire entre les espaces de vecteurs liés
![]() et
et
![]() , qui est de plus indépendante du point
, qui est de plus indépendante du point ![]() .
.
![]() est une translation ou une homothéthie de rapport
est une translation ou une homothéthie de rapport ![]() ,
,
![]() est
est
![]() ou
ou
![]() respectivement.
respectivement.
![]() et
et
![]() sont des apllications affines, alors
sont des apllications affines, alors
![]() et une droite
et une droite
![]() non parallèle à
non parallèle à ![]() . Le symétrique de
. Le symétrique de
![]() par rapport à
par rapport à ![]() parallèlement à
parallèlement à
![]() est l'unique point
est l'unique point
![]() formant avec
formant avec ![]() un segment parallèle à
un segment parallèle à
![]() et dont le milieu appartient à
et dont le milieu appartient à ![]() .
L'application
.
L'application
![]() est une affinité. En effet, dans un repère
est une affinité. En effet, dans un repère
![]() où
où ![]() est le point de
percée de
est le point de
percée de
![]() dans
dans ![]() , où
, où
![]() est une base de
est une base de
![]() et
et ![]() est un vecteur-directeur de
est un vecteur-directeur de
![]() , elle est représentée
sous la forme (21) avec
, elle est représentée
sous la forme (21) avec
![]() et
et
![]() et une droite
et une droite
![]() non parallèle à
non parallèle à ![]() . La projection de
. La projection de
![]() sur
sur ![]() parallèlement à
parallèlement à
![]() est le
point de percée
est le
point de percée
![]() dans
dans ![]() de la droite passant par
de la droite passant par ![]() et parallèle à
et parallèle à
![]() (5.3). L'application
(5.3). L'application
![]() est
affine car, dans un repère comme dans l'exemple précédent, elle est représentée sous la forme (21) avec
est
affine car, dans un repère comme dans l'exemple précédent, elle est représentée sous la forme (21) avec
![]() et
et
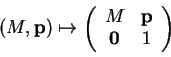
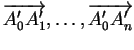 et pour
et pour 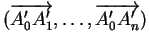 soit une base. Ceci équivaut au fait que
soit une base. Ceci équivaut au fait que