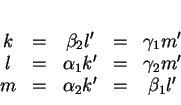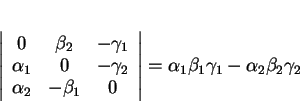Théorème 2.5.7
(Ceva)
Soient un triangle
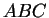
et des points
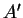
,
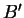
et
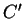
choisis respectivement
sur
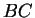
,
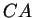
et
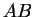
. Les droites
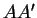
,
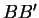
et
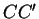
sont concourantes
ou parallèles si et seulement si
Remarque 2.5.8
Comme à propos du théorème de Ménélaüs, pour éviter les cas où un rapport de section n'existe pas, on peut formuler la condition de l'énoncé au moyen
des coordonnées barycentriques
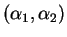
, etc. des points
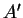
,
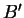
,
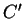
. Elle s'écrit alors :
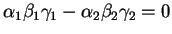
.
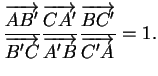
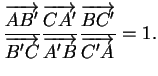
![]() , les plans
, les plans
![]() ,
,
![]() et
et
![]() ont une droite en
commun si et seulement si ils ont un vecteur directeur commun, c'est-à-dire si il existe des nombres
ont une droite en
commun si et seulement si ils ont un vecteur directeur commun, c'est-à-dire si il existe des nombres
![]() tels que
tels que