



suivant: 7.4.0.1 Plan tangent
monter: 7.4 Plan tangent, orientation
précédent: 7.4.0.0.1 Notations
Table des matières
a)Puisque
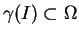 , on a
, on a
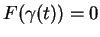 pour tout
pour tout 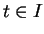 . En dérivant par rapport à
. En dérivant par rapport à 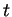 ,
cela donne
,
cela donne
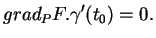 |
(7.3) |
b)Puisque
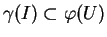 , il existe des fonctions
, il existe des fonctions
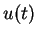 et
et 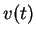 définies dans
définies dans 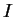 telles que, pour tout
telles que, pour tout 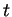 ,
,
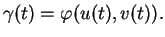 |
(7.4) |
Figure:
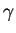 est composé de
est composé de 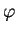 et de d'une courbe dans
et de d'une courbe dans 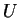 .
.
|
|
Ces fonctions sont de classe 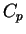 , comme
, comme 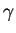 .
C'est évident si
.
C'est évident si
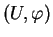 est un paramétrage par des coordonnées,
car alors
est un paramétrage par des coordonnées,
car alors 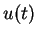 et
et 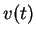 sont simplement deux des coordonnées de
sont simplement deux des coordonnées de
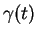 dans un repère de
dans un repère de
 . Sinon,
. Sinon,
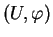 est
localement équivalent à un paramétrage par des coordonnées;
est
localement équivalent à un paramétrage par des coordonnées; 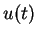 et
et 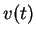 sont alors de classe
sont alors de classe 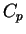 car ils sont images de deux coordonnées
de
car ils sont images de deux coordonnées
de 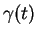 par le changement de paramètres exprimant l'équivalence.
On a donc, en dérivant aussi par rapport à
par le changement de paramètres exprimant l'équivalence.
On a donc, en dérivant aussi par rapport à 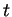 ,
,
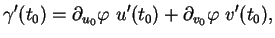 |
(7.5) |
où
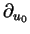 et
et
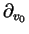 représentent les
dérivées par rapport à
représentent les
dérivées par rapport à 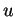 et
et 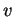 évaluées en
évaluées en
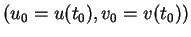 respectivement.
respectivement.




suivant: 7.4.0.1 Plan tangent
monter: 7.4 Plan tangent, orientation
précédent: 7.4.0.0.1 Notations
Table des matières
2002-12-17
![]() , on a
, on a
![]() pour tout
pour tout ![]() . En dérivant par rapport à
. En dérivant par rapport à ![]() ,
cela donne
,
cela donne
![]() , il existe des fonctions
, il existe des fonctions
![]() et
et ![]() définies dans
définies dans ![]() telles que, pour tout
telles que, pour tout ![]() ,
,