



suivant: 3.2.3 Bases orthonormées
monter: 3.2.2 Longueur et angle
précédent: 3.2.2.1 Longueur
Table des matières
Le nombre
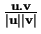 est donc compris entre
est donc compris entre 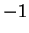 et
et 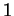 (on suppose que
(on suppose que 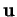 et
et 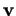 ne sont pas nuls).
Par conséquent, il existe un angle
ne sont pas nuls).
Par conséquent, il existe un angle
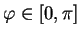 dont c'est le cosinus. C'est l'angle (non orienté) entre
dont c'est le cosinus. C'est l'angle (non orienté) entre
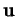 et
et 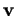 . Ainsi, par définition de celui-ci,
. Ainsi, par définition de celui-ci,
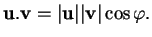 |
(3.2) |
Figure:
Angle non orienté.
|
|
En particulier, des vecteurs 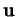 et
et 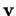 sont dits orthogonaux ou perpendiculaires si
sont dits orthogonaux ou perpendiculaires si
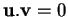 car alors, s'ils ne sont pas nuls, ils forment un angle droit. On note
car alors, s'ils ne sont pas nuls, ils forment un angle droit. On note
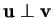 le fait que
le fait que 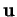 et
et 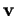 sont orhogonaux. Ayant en mémoire les formules des triangles rectangles(3.2), on peut interpréter la relation précédente en disant que
sont orhogonaux. Ayant en mémoire les formules des triangles rectangles(3.2), on peut interpréter la relation précédente en disant que
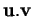 est le produit de la longueur de
est le produit de la longueur de 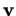 et de la mesure algébrique de la projection
orthogonale de
et de la mesure algébrique de la projection
orthogonale de
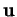 sur
sur 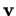 . Dans le même registre, la quantité calculée en (15) vaut
qui est le carré de l'aire du ``parallélogramme" déterminé par les vecteurs
. Dans le même registre, la quantité calculée en (15) vaut
qui est le carré de l'aire du ``parallélogramme" déterminé par les vecteurs 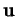 et
et 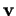 .
.




suivant: 3.2.3 Bases orthonormées
monter: 3.2.2 Longueur et angle
précédent: 3.2.2.1 Longueur
Table des matières
2002-12-17
![]() est donc compris entre
est donc compris entre ![]() et
et ![]() (on suppose que
(on suppose que ![]() et
et ![]() ne sont pas nuls).
Par conséquent, il existe un angle
ne sont pas nuls).
Par conséquent, il existe un angle
![]() dont c'est le cosinus. C'est l'angle (non orienté) entre
dont c'est le cosinus. C'est l'angle (non orienté) entre
![]() et
et ![]() . Ainsi, par définition de celui-ci,
. Ainsi, par définition de celui-ci,