2.5.3 Le théorème de Menelaüs

Figure: Le théorème de Menelaüs.

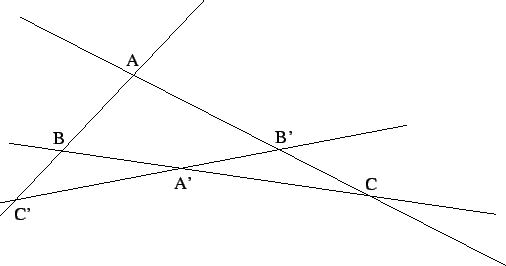
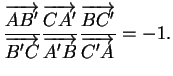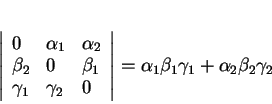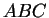
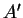
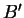
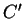
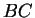
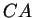
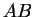
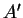
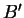
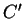
Théorème 2.5.4   (Menelaüs) Soient un triangle $ABC$ et des points $A'$, $B'$ et $C'$ choisis respectivement sur $BC$, $CA$ et $AB$. Les points $A'$, $B'$ et $C'$ sont alignés si et seulement si

$$\frac{\overrightarrow{AB'}}{\overrightarrow{B'C}}\frac{\overright... ...}{\overrightarrow{A'B}}\frac{\overrightarrow{BC'}}{\overrightarrow{C'A}} = -1.$$

Preuve. Choisissons pour origine un point $S$ extérieur au plan du triangle $ABC$. Les vecteurs positions $\bf a$, $\bf b$ et $\bf c$ de $A$, $B$ et $C$ sont linéairement indépendants sinon les droites $SA$, $SB$, et $SC$ seraient dans un plan et les points $A$, $B$ et $C$ seraient alignés le long de l'intersection de ce plan avec celui du triangle $ABC$.

Figure: Si $A'$, $B'$ et $C'$ sont alignés, les droites $SA'$, $SB'$ et $SC'$ sont coplanaires.

Les vecteurs positions $\bf a'$, $\bf b'$ et $\bf c'$ de $A'$, $B'$ et $C'$ s'écrivent

$$\left\{ \begin{array}{lll} {\bf a'} ... ...f a} \\ {\bf c'} & = & \gamma_1{\bf a}+\gamma_2{\bf b} \\ \end{array} \right.$$ (2.2)

avec $\alpha_1+\alpha_2=\beta_1+\beta_2=\gamma_1+\gamma_2=1$. Tout revient à démontrer que $\bf a'$, $\bf b'$, $\bf c'$ sont linéairement dépendants si et seulement si $\alpha_1\beta_1\gamma_1+\alpha_2\beta_2\gamma_2=0$. On tire facilement de (10) que

$$\left\{ \begin{array}{lll} (\alpha_1... ...f a'}+\alpha_1\gamma_1{\bf b'}- \alpha_1\beta_2{\bf c'} \\ \end{array} \right.$$ (2.3)

Donc, si $\alpha_1\beta_1\gamma_1+\alpha_2\beta_2\gamma_2 \ne 0$, alors $\bf a$, $\bf b$, $\bf c$ sont combinaisons linéaires de $\bf a'$, $\bf b'$, $\bf c'$ qui ne sont dès lors pas linéairement dépendants. Par contre, si $\alpha_1\beta_1\gamma_1+\alpha_2\beta_2\gamma_2=0$, alors, comme les coefficients de $\bf a'$, $\bf b'$, $\bf c'$ dans (11) ne sont pas tous nuls, $\bf a'$, $\bf b'$, $\bf c'$ sont linéairement dépendants. $\qed$

Remarque 2.5.5   Variante utilisant les déterminants. Vu (10), $\bf a'$, $\bf b'$, $\bf c'$ sont linéairement dépendants si et seulement si le déterminant

$$% latex2html id marker 29964\left \vert \begin{array}{lll}... ... \right \vert =\alpha_1\beta_1\gamma_1+\alpha_2\beta_2\gamma_2$$

est nul.

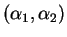
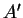
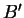
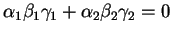
Remarque 2.5.6   Pour éviter les cas où un rapport de section n'existe pas, on peut formuler la condition de l'énoncé à l'aide des coordonnées barycentriques $(\alpha_1,\alpha_2)$, etc. des points $A'$, $B'$, $C'$. Elle s'écrit alors simplement: $\alpha_1\beta_1\gamma_1+\alpha_2\beta_2\gamma_2=0$.