



suivant: 3.3.1 Définition
monter: 3 Introduction aux espaces
précédent: 3.2.4 Complément orthogonal
Table des matières
Il y a généralement deux déterminations de 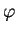 vérifiant la formule (16) dans
vérifiant la formule (16) dans
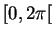 et cette ambiguïté a été levée en précisant que
l'angle non orienté de deux vecteurs
et cette ambiguïté a été levée en précisant que
l'angle non orienté de deux vecteurs 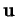 et
et 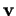 doit être compris entre 0 et
doit être compris entre 0 et 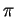 . Intuitivement les deux déterminations représentent malgré tout chacune
quelque chose. Elles correspondent aux deux manières de faire pivoter
. Intuitivement les deux déterminations représentent malgré tout chacune
quelque chose. Elles correspondent aux deux manières de faire pivoter 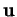 dans le plan vectoriel qu'il forme avec
dans le plan vectoriel qu'il forme avec 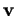 (3.3): dans le ``sens des aiguilles d'une montre" ou
dans le sens ``opposé", afin qu'il prenne même direction et même sens que
(3.3): dans le ``sens des aiguilles d'une montre" ou
dans le sens ``opposé", afin qu'il prenne même direction et même sens que 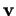 . Selon le sens
adopté, c'est un angle d'amplitude
. Selon le sens
adopté, c'est un angle d'amplitude 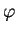 , ou
, ou
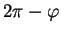 qui est balayé.
qui est balayé.
C'est dans le but de modéliser ces deux sens possibles, indispensables dans la description de nombreux phénomènes physiques (éléctricité,
magnétisme, gravitation,...), que l'on introduit la notion d'orientation. En dimension 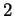 , le problème se résume à choisir un des sens de rotation. Un
élément supplémentaire vient se greffer en dimension
, le problème se résume à choisir un des sens de rotation. Un
élément supplémentaire vient se greffer en dimension 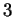 . En effet, toujours intuitivement, en dimension
. En effet, toujours intuitivement, en dimension 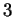 , un plan partage
, un plan partage  en deux demi-espaces dont il faut
encore préciser lequel est ``au-dessus" de ce plan pour décrire la manière dont on tourne dans celui-ci: le sens d'un même mouvement giratoire plan n'est pas le
même ``vu du dessus" que ``du dessous".
en deux demi-espaces dont il faut
encore préciser lequel est ``au-dessus" de ce plan pour décrire la manière dont on tourne dans celui-ci: le sens d'un même mouvement giratoire plan n'est pas le
même ``vu du dessus" que ``du dessous".
Figure:
La tête à l'envers...
|
|
Sur Terre, quelqu'un définit les ``au-dessus" et ``en-dessous" du lieu où il se trouve grâce à la pesanteur. Le champ magnétique terrestre permet de compléter
l'orientation locale en indiquant le nord, l'est et l'ouest étant reconnu grâce à son aptitude à discerner la gauche et la droite. On peut aussi définir l'orientation de la Terre par le champ magnétique qui précise ce qui est au-dessus et en-dessous de l'équateur, le plan de l'équateur étant ensuite orienté à l'aide du mouvement de rotation de la Terre.
Tout revient donc à se donner une base locale dont les trois éléments servent à préciser ce qui est ``à gauche, à droite", ``devant, derrière" et ``en haut, en bas".
Il est assez clair que deux bases définissent la même orientation lorsqu'on peut appliquer l'une sur l'autre par un mouvement continu.
Sous-sections




suivant: 3.3.1 Définition
monter: 3 Introduction aux espaces
précédent: 3.2.4 Complément orthogonal
Table des matières
2002-12-17
![]() , le problème se résume à choisir un des sens de rotation. Un
élément supplémentaire vient se greffer en dimension
, le problème se résume à choisir un des sens de rotation. Un
élément supplémentaire vient se greffer en dimension ![]() . En effet, toujours intuitivement, en dimension
. En effet, toujours intuitivement, en dimension ![]() , un plan partage
, un plan partage ![]() en deux demi-espaces dont il faut
encore préciser lequel est ``au-dessus" de ce plan pour décrire la manière dont on tourne dans celui-ci: le sens d'un même mouvement giratoire plan n'est pas le
même ``vu du dessus" que ``du dessous".
en deux demi-espaces dont il faut
encore préciser lequel est ``au-dessus" de ce plan pour décrire la manière dont on tourne dans celui-ci: le sens d'un même mouvement giratoire plan n'est pas le
même ``vu du dessus" que ``du dessous".