



suivant: 2.3 Combinaisons affines
monter: 2.2 Espaces affines
précédent: 2.2.2 Exemple
Table des matières
Soit un point  de
de
 . Les vecteurs liés en
. Les vecteurs liés en  sont les couples
sont les couples 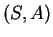 ,
,
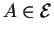 .
La correspondance
.
La correspondance
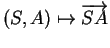 est manifestement une bijection entre l'ensemble
est manifestement une bijection entre l'ensemble
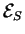 des vecteurs liés en
des vecteurs liés en  et
et
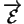 . Par conséquent,
. Par conséquent,
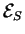 est un espace vectoriel pour les opérations
est un espace vectoriel pour les opérations
Dans la mesure où les éléments de
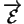 représentent les translations de
représentent les translations de
 , il est légitime de dire que quatre points
, il est légitime de dire que quatre points  ,
, 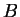 ,
, 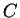 ,
, 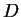
Figure:
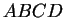 est un parallélogramme car
est un parallélogramme car 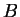 et
et 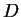 sont les images de
sont les images de  et
et 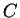 par une même translation.
par une même translation.
|
|
forment un parallélogramme 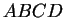 si
si
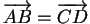 (on dit alors que les éléments
(on dit alors que les éléments 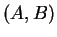 et
et 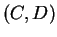 de
de
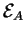 et
et
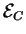 sont équipollents). L'addition dans
sont équipollents). L'addition dans
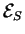 se fait suivant la ``règle du parallélogramme". En effet, si
se fait suivant la ``règle du parallélogramme". En effet, si
alors 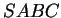 est un parallélogramme puisque
est un parallélogramme puisque
L'origine  étant fixée, les vecteurs
étant fixée, les vecteurs
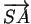 ,
,
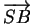 , ... sont les vecteurs-positions des points
, ... sont les vecteurs-positions des points  ,
, 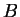 , etc.
, etc.
Figure:
Dans
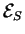 , l'addition résulte de la règle du parallélogramme.
, l'addition résulte de la règle du parallélogramme.
|
|




suivant: 2.3 Combinaisons affines
monter: 2.2 Espaces affines
précédent: 2.2.2 Exemple
Table des matières
2002-12-17
![]() si
si
![]() (on dit alors que les éléments
(on dit alors que les éléments ![]() et
et ![]() de
de
![]() et
et
![]() sont équipollents). L'addition dans
sont équipollents). L'addition dans
![]() se fait suivant la ``règle du parallélogramme". En effet, si
se fait suivant la ``règle du parallélogramme". En effet, si
![]() étant fixée, les vecteurs
étant fixée, les vecteurs
![]() ,
,
![]() , ... sont les vecteurs-positions des points
, ... sont les vecteurs-positions des points ![]() ,
, ![]() , etc.
, etc.