suivant: 7.2.0.3 Paramétrages équivalents
monter: 7.2 Paramétrage - Portion
précédent: 7.2.0.1 Paramétrage
Table des matières
L'image
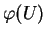 d'un
paramétrage
d'un
paramétrage
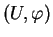 de classe
de classe 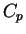 est une portion régulière de surface de classe
est une portion régulière de surface de classe 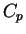 . Dans le cas d'un paramétrage par des coordonnées, c'est le graphe de la fonction exprimant la
troisième coordonnées à l'aide des deux qui servent de paramètres.
. Dans le cas d'un paramétrage par des coordonnées, c'est le graphe de la fonction exprimant la
troisième coordonnées à l'aide des deux qui servent de paramètres.
Figure:
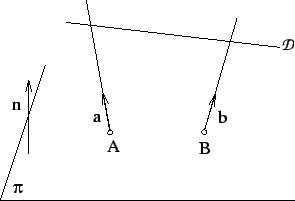
 engendre un paraboloïde hyperbolique.
engendre un paraboloïde hyperbolique.
|
|
Soient deux droites gauches
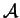 et
et
 perçant un plan
perçant un plan 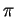 en les points
en les points  et
et 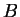 respectivement. Les points situés sur les droites parallèles à
respectivement. Les points situés sur les droites parallèles à 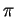 ets'appuyant sur
ets'appuyant sur
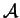 et
et
 sont exactement les points de la forme
sont exactement les points de la forme
où 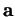 est un vecteur-directeur de
est un vecteur-directeur de
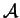 ,
, 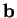 un de
un de
 et
et 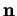 est une normale à
est une normale à 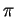 ,
, 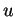 et
et 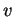 étant des nombres réels arbitraires. Les vecteurs
étant des nombres réels arbitraires. Les vecteurs
sont linéairement indépendants pour tout 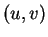 . Par conséquent,
. Par conséquent,
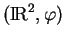 est un paramétrage. La portion régulière de surface qu'il décrit est un paraboloïde hyperbolique.
est un paramétrage. La portion régulière de surface qu'il décrit est un paraboloïde hyperbolique.
Exemple 7.2.2
Sphère et projection stéréographique
Figure:
 est la projection stéréographique de
est la projection stéréographique de  .
.
|
|
Soit 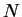 un point de la sphère
un point de la sphère
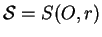 . Si
. Si
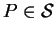 est distinct de
est distinct de 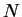 , la droite
, la droite 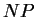 perce le plan équatorial
perce le plan équatorial
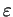 relatif à
relatif à 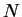 (c'est-à-dire passant par
(c'est-à-dire passant par 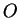 et perpendiculaire à
et perpendiculaire à 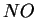 ) en un seul point
) en un seul point  . Il est clair que le passage de
. Il est clair que le passage de  à
à  est une bijection entre
est une bijection entre
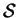 privé de
privé de 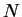 et
et
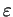 . On l'appelle la projection stéréographique à partir de
. On l'appelle la projection stéréographique à partir de 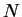 . On obtient alors un paramétrage de
. On obtient alors un paramétrage de
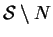 en reconstituant
en reconstituant  à partir de
à partir de  . Le repère étant choisi comme indiqué sur la figure, cela donne le paramétrage
. Le repère étant choisi comme indiqué sur la figure, cela donne le paramétrage
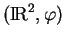 , où
, où
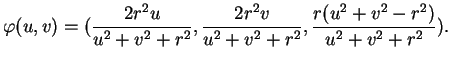 |
(7.2) |
Exemple 7.2.3
L'hémisphère sud
Figure:
Changement de paramétrages dans l'hémisphère sud.
|
|
L' ``hémisphère sud" de
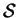 (celui dont les points ont une cote
(celui dont les points ont une cote 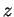 négative) peut également être décrit au moyen d'un paramétrage par des coordonnées. Dans le repère considéré, la sphère est en effet le lieu des points dont les coordonnées vérifient l'équation
négative) peut également être décrit au moyen d'un paramétrage par des coordonnées. Dans le repère considéré, la sphère est en effet le lieu des points dont les coordonnées vérifient l'équation
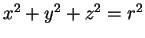 . L'hémisphère sud admet donc le paramétrage
. L'hémisphère sud admet donc le paramétrage 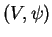 , où
est défini dans le disque ouvert
, où
est défini dans le disque ouvert
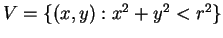 .
.




suivant: 7.2.0.3 Paramétrages équivalents
monter: 7.2 Paramétrage - Portion
précédent: 7.2.0.1 Paramétrage
Table des matières
2002-12-17