



suivant: 7.4.0.2 Orientation et normale
monter: 7.4 Plan tangent, orientation
précédent: 7.4.0.0.2 Observations
Table des matières
Puisque 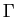 est tracé sur
est tracé sur  , son vecteur tangent
, son vecteur tangent
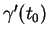 est dit tangent à
est dit tangent à  en
en  . Il est commode de déclarer également que
. Il est commode de déclarer également que 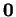 est tangent à
est tangent à  en
en  .
.
Proposition 7.4.1
L'ensemble

des vecteurs tangents à

en

est
le plan vectoriel
de
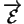
.
Preuve. Vu (36),
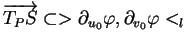 .
Inversement, on a
.
Inversement, on a
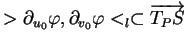 car si
car si
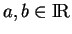 , on a
Ceci montre que
, on a
Ceci montre que
 est l'enveloppe linéaire de
est l'enveloppe linéaire de
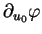 et
et
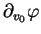 . C'est donc un
sous espace vectoriel de dimension deux de
. C'est donc un
sous espace vectoriel de dimension deux de
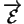 puisque ces
vecteurs sont linéairement indépendants. Vu (34),
Ces deux sous-espaces sont donc égaux car leurs dimensions sont
égales.
puisque ces
vecteurs sont linéairement indépendants. Vu (34),
Ces deux sous-espaces sont donc égaux car leurs dimensions sont
égales.
Figure:
Plan tangent à  .
.
|
|
Le plan tangent à  en
en  est par définition le plan
est par définition le plan
Par exemple, le plan tangent à la sphère 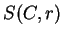 en
en  est le plan
passant par
est le plan
passant par  et perpendiculaire à
et perpendiculaire à 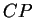 . On a observé en effet que
. On a observé en effet que 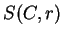 admet une équation cartésienne dont le gradient en
admet une équation cartésienne dont le gradient en  est
est
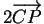 .
.
La proposition précédente montre que 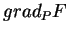 est une normale au
plan tangent en
est une normale au
plan tangent en  de
de  . Par conséquent,
. Par conséquent,
Proposition 7.4.2
Dans tout repère orthonormé de

, le plan tangent à

en le
point

de coordonnées
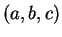
admet l'équation cartésienne




suivant: 7.4.0.2 Orientation et normale
monter: 7.4 Plan tangent, orientation
précédent: 7.4.0.0.2 Observations
Table des matières
2002-12-17
![]() est tracé sur
est tracé sur ![]() , son vecteur tangent
, son vecteur tangent
![]() est dit tangent à
est dit tangent à ![]() en
en ![]() . Il est commode de déclarer également que
. Il est commode de déclarer également que ![]() est tangent à
est tangent à ![]() en
en ![]() .
.
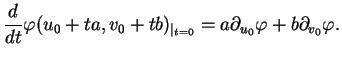
![]() en
en ![]() est par définition le plan
est par définition le plan
![]() est une normale au
plan tangent en
est une normale au
plan tangent en ![]() de
de ![]() . Par conséquent,
. Par conséquent,