Remarque 6.3.3
Il est possible qu'un même point de
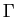
corresponde à plusieurs valeurs du paramètre
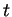
. L'arc
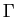
admet alors éventuellement plusieurs tangentes en
ce point. C'est par exemple le cas du
folium de Descartes. Dans un repère orthonormé du plan, celui-ci admet le paramétrage
Figure 4:
Le folium de Descartes.
|
|
L'origine du repère est obtenue en 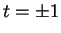 et il y a deux tangentes en ce point, de vecteurs-directeurs de composantes
et il y a deux tangentes en ce point, de vecteurs-directeurs de composantes
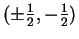 .
.
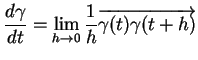
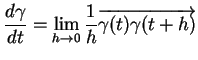
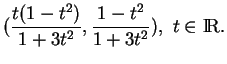
![]() et il y a deux tangentes en ce point, de vecteurs-directeurs de composantes
et il y a deux tangentes en ce point, de vecteurs-directeurs de composantes
![]() .
.