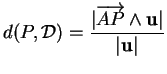suivant: 4.4.2.3 Distance de deux
monter: 4.4.2 Distance entre variétés
précédent: 4.4.2.1 Distance d'un point
Table des matières
La distance d'un point  à une droite
à une droite
 est également réalisée en un point unique
est également réalisée en un point unique 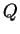 de
de
 caractérisé
par le fait que
caractérisé
par le fait que 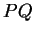 soit perpendiculaire à
soit perpendiculaire à
 (4.3).
Nous allons obtenir la formule donnant cette distance lorsque
(4.3).
Nous allons obtenir la formule donnant cette distance lorsque
 est de dimension
est de dimension 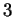 et orienté.
Supposons
et orienté.
Supposons
 donné par un de ses points
donné par un de ses points  et un vecteur-directeur
et un vecteur-directeur 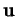 . Le point
. Le point 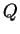 est cette fois de la forme
est cette fois de la forme
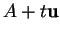 où
où 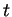 est univoquement déterminé par
la condition
est univoquement déterminé par
la condition
Le point 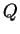 s'appelle encore la projection orthogonale de
s'appelle encore la projection orthogonale de  sur
sur
 . Il se note
. Il se note
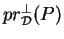 .
Cela étant, dans le triangle
.
Cela étant, dans le triangle 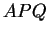 rectangle en Q,
rectangle en Q,
Par conséquent,
(cf. Proposition 3.5), formule qui vaut encore quand  est sur
est sur
 .
.
Figure 5:
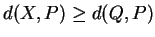 .
.
|
|




suivant: 4.4.2.3 Distance de deux
monter: 4.4.2 Distance entre variétés
précédent: 4.4.2.1 Distance d'un point
Table des matières
2002-12-17
![]() à une droite
à une droite
![]() est également réalisée en un point unique
est également réalisée en un point unique ![]() de
de
![]() caractérisé
par le fait que
caractérisé
par le fait que ![]() soit perpendiculaire à
soit perpendiculaire à
![]() (4.3).
Nous allons obtenir la formule donnant cette distance lorsque
(4.3).
Nous allons obtenir la formule donnant cette distance lorsque
![]() est de dimension
est de dimension ![]() et orienté.
Supposons
et orienté.
Supposons
![]() donné par un de ses points
donné par un de ses points ![]() et un vecteur-directeur
et un vecteur-directeur ![]() . Le point
. Le point ![]() est cette fois de la forme
est cette fois de la forme
![]() où
où ![]() est univoquement déterminé par
la condition
est univoquement déterminé par
la condition