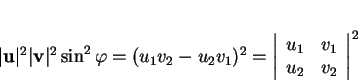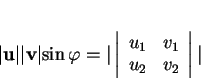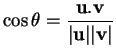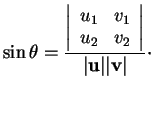suivant: 3.3.2.1 Angles à côtés
monter: 3.3 Orientation, en dimensions
précédent: 3.3.1 Définition
Table des matières
Supposons que  est de dimension
est de dimension 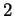 et qu'il est orienté.
Soient une base orthonormée positive
et qu'il est orienté.
Soient une base orthonormée positive
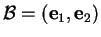 et
et
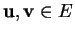 formant l'angle non orienté
formant l'angle non orienté 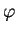 .
Il est facile de vérifier à l'aide de la formule (16) que
.
Il est facile de vérifier à l'aide de la formule (16) que
où les 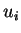 et les
et les 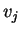 sont les composantes de
sont les composantes de 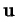 et
et 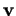 selon
selon
 . Donc, puisque
. Donc, puisque
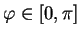 ,
,
Ainsi, si 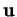 et
et 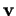 forment une base positive, on passe de
forment une base positive, on passe de 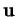 à
à
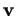 dans ``le sens de l'orientation" et
dans ``le sens de l'orientation" et 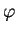 représente l'angle orienté
formé par
représente l'angle orienté
formé par 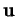 et
et 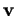 , car alors le déterminant figurant dans cette égalité est positif. Dans le cas contraire, il est négatif, on passe de
, car alors le déterminant figurant dans cette égalité est positif. Dans le cas contraire, il est négatif, on passe de 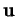 à
à 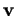 dans le
``sens opposé" à celui de l'orientation et l'angle orienté formé par
dans le
``sens opposé" à celui de l'orientation et l'angle orienté formé par 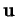 et
et 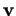 est
est
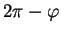 .
L'angle orienté
.
L'angle orienté 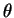 de
de 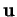 et
et 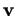 est donc univoquement déterminé par les conditions
et
Il dépend bien entendu de l'ordre de
est donc univoquement déterminé par les conditions
et
Il dépend bien entendu de l'ordre de 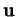 et
et 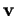 .
.
Figure:
Angles orientés (sens trigonométrique).
|
|
Il y a deux orientations possible de  . En physique, l'une correspond au sens des aiguilles d'une montre. L'autre correspond à l'orientation conventionnelle du
``cercle trigonométrique" quand on le dessine effectivement.
. En physique, l'une correspond au sens des aiguilles d'une montre. L'autre correspond à l'orientation conventionnelle du
``cercle trigonométrique" quand on le dessine effectivement.
Sous-sections




suivant: 3.3.2.1 Angles à côtés
monter: 3.3 Orientation, en dimensions
précédent: 3.3.1 Définition
Table des matières
2002-12-17
![]() est de dimension
est de dimension ![]() et qu'il est orienté.
Soient une base orthonormée positive
et qu'il est orienté.
Soient une base orthonormée positive
![]() et
et
![]() formant l'angle non orienté
formant l'angle non orienté ![]() .
Il est facile de vérifier à l'aide de la formule (16) que
.
Il est facile de vérifier à l'aide de la formule (16) que