Supposons que la dimension de
![]() soit
soit ![]() .
.
(i) Les points fixes de
![]() forment une droite, l' axe (de rotation) de
forment une droite, l' axe (de rotation) de
![]() .
.
(ii) Dans un repère orthonormé positif
![]() , où
, où ![]() est un vecteur-directeur de
l'axe de rotation de
est un vecteur-directeur de
l'axe de rotation de
![]() ,
,
![]() est représenté par
est représenté par
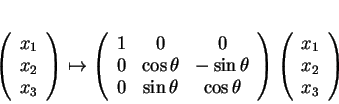
Preuve. (i) Il est clair qu'un vecteur-directeur d'une droite de points fixes de
![]() est un vecteur propre de
est un vecteur propre de
![]() de valeur propre
de valeur propre ![]() . Réciproquement,
une droite passant par
. Réciproquement,
une droite passant par ![]() et admettant un vecteur-directeur qui est un vecteur propre de valeur propre
et admettant un vecteur-directeur qui est un vecteur propre de valeur propre ![]() de
de
![]() est une droite de points fixes de
est une droite de points fixes de
![]() . Comme la dimension de
. Comme la dimension de
![]() est
est ![]() ,
,
![]() admet trois valeurs propres (comptées avec leurs multiplicités): une est réelle et les deux autres sont
soit réelles soit complexes et conjuguées l'une de l'autre. Puisque
admet trois valeurs propres (comptées avec leurs multiplicités): une est réelle et les deux autres sont
soit réelles soit complexes et conjuguées l'une de l'autre. Puisque
![]() est une application orthogonale, ses valeurs propres réelles sont
est une application orthogonale, ses valeurs propres réelles sont ![]() . Son
déterminant étant positif,
. Son
déterminant étant positif, ![]() est une valeur propre simple ou bien une valeur propre triple. Dans ce dernier cas,
est une valeur propre simple ou bien une valeur propre triple. Dans ce dernier cas,
![]() est
est
![]() et dans le premier, il
admet exactement une droite de points fixes.
et dans le premier, il
admet exactement une droite de points fixes.
(ii) Les plans perpendiculaires à l'axe
![]() de rotation sont stabilisés par
de rotation sont stabilisés par
![]() . En particulier, la restriction de
. En particulier, la restriction de
![]() au plan
au plan
![]() est une rotation plane. On voit que
est une rotation plane. On voit que
![]() est représenté de la façon indiquée en appliquant la Proposition 3.4. L'angle
est représenté de la façon indiquée en appliquant la Proposition 3.4. L'angle ![]() est alors l'angle
orienté entre
est alors l'angle
orienté entre
![]() et
et
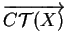 ,
,
![]() ,
, ![]() étant rapporté au repère
étant rapporté au repère
![]() . L'axe
. L'axe
![]() n'a que deux vecteurs-directeurs
normés:
n'a que deux vecteurs-directeurs
normés:
![]() et
et
![]() . Si l'on remplace
. Si l'on remplace
![]() par
par
![]() , il faut encore échanger
, il faut encore échanger ![]() et
et ![]() pour conserver un repère positif de
pour conserver un repère positif de
![]() , ce qui a pour effet de changer l'orientation de
, ce qui a pour effet de changer l'orientation de ![]() et donc
de remplacer
et donc
de remplacer ![]() par
par
![]() .
.![]()