



suivant: 2.4.3 Direction
monter: 2.4 Variétés affines
précédent: 2.4.1 Deux axiomes d'Euclide
Table des matières
Une variété affine de
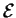 est une partie
est une partie
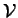 de
de
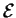 qui contient les droites passant par deux quelconques de ses points:
qui contient les droites passant par deux quelconques de ses points:
Remarque 2.4.1
L'ensemble vide
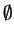
et les points de
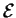
sont des variétés affines car ils ne contiennent pas deux points distincts.
Proposition 2.4.2
Une partie
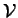
de
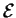
est une variété affine si et seulement si elle contient les combinaisons affines de ses points.
Preuve. Si
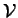 contient les combinaisons affines de ses points, alors il contient en particulier les droites qui joignent deux quelconques de ses points.
Inversement, le calcul des barycentres de plusieurs points se ramenant par groupement successifs à des calculs de barycentres de deux points (Proposition 3.4), si
contient les combinaisons affines de ses points, alors il contient en particulier les droites qui joignent deux quelconques de ses points.
Inversement, le calcul des barycentres de plusieurs points se ramenant par groupement successifs à des calculs de barycentres de deux points (Proposition 3.4), si
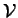 est une variété affine, alors il contient les combinaisons affines de ses éléments.
est une variété affine, alors il contient les combinaisons affines de ses éléments.
Figure:
Le barycentre de 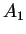 , ... ,
, ... , 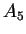 est calculé progressivement en remplaçant
est calculé progressivement en remplaçant 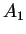 et
et 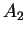 par leur barycentre
par leur barycentre 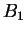 ,
, 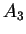 et
et 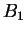 par le leur,... A chaque étape, les poids sont ajustés.
par le leur,... A chaque étape, les poids sont ajustés.
|
|
Proposition 2.4.3
Soient des points
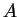
,
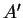
de
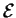
et des sous-espaces vectoriels
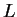
et
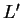
de
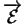
.
(i) L'ensemble
est une variété affine de
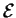
, contenant
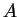
.
(ii) On a  si et seulement si
si et seulement si
 et
et  .
.
Preuve. (i) Montrons que si
 sont distincts, alors la droite
sont distincts, alors la droite 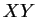 est contenue dans
est contenue dans 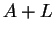 . Il existe
. Il existe
 tels que
tels que
 et
et
 . On a
et par conséquent,
. On a
et par conséquent,
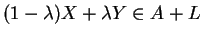 vu la Proposition 3.2. Donc
vu la Proposition 3.2. Donc
 . Bien entendu,
. Bien entendu,
 .
.
(ii) Supposons que  . Puisque
. Puisque  , il existe
, il existe
 tel que
tel que
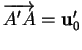 .
De plus, si
.
De plus, si
 , alors il existe
, alors il existe
 tel que
tel que
 si bien que
si bien que
Donc
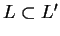 et, par symétrie,
et, par symétrie,
 .
.
Inversement, supposons que
 et
et  . Soit
. Soit
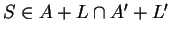 . Pour tout
. Pour tout
 , on a
, on a
puisque
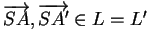 . Donc,
. Donc,
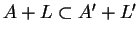 et, par symétrie,
et, par symétrie,
 .
.




suivant: 2.4.3 Direction
monter: 2.4 Variétés affines
précédent: 2.4.1 Deux axiomes d'Euclide
Table des matières
2002-12-17

![]() si et seulement si
si et seulement si
![]() et
et ![]() .
.
![]() . Puisque
. Puisque ![]() , il existe
, il existe
![]() tel que
tel que
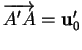 .
De plus, si
.
De plus, si
![]() , alors il existe
, alors il existe
![]() tel que
tel que
![]() si bien que
si bien que

![]() et
et ![]() . Soit
. Soit
![]() . Pour tout
. Pour tout
![]() , on a
, on a


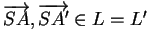 . Donc,
. Donc,