



suivant: 7.2.0.2 Portion régulière de
monter: 7.2 Paramétrage - Portion
précédent: 7.2 Paramétrage - Portion
Table des matières
Un paramétrage (de dimension 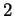 )
est la donnée
)
est la donnée
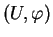 d'une application de classe
d'une application de classe 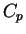 d'un ouvert
d'un ouvert 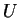 de
de
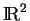 dans
dans
 , injective et dont la dérivée
, injective et dont la dérivée 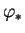 est injective partout dans
est injective partout dans
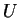 .
.
Dans un repère
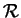 de
de
 , les trois composantes
, les trois composantes
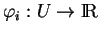 ,
, 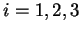 , de
, de 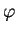 sont des fonctions de classe
sont des fonctions de classe 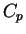 et la condition sur
et la condition sur 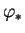 signifie très exactement que les vecteurs
signifie très exactement que les vecteurs
sont linéairement indépendants en tout point 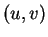 de
de 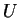 . Cette condition s'écrit aussi
. Cette condition s'écrit aussi
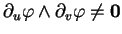 |
|
|
(7.1) |
Lorsque les paramètres 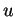 et
et 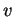 sont deux des coordonnées, on dit que
sont deux des coordonnées, on dit que
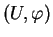 est un paramétrage par des coordonnées. Par exemple, si
est un paramétrage par des coordonnées. Par exemple, si 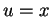 et
et 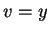 , alors
, alors 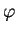 est de la forme
où
est de la forme
où 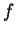 est une fonction de classe
est une fonction de classe 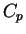 . La condition (32) est alors automatiquement satisfaite puisque
. La condition (32) est alors automatiquement satisfaite puisque
Figure:
Paramétrage par des coordonnées.
|
|
Figure:
Paramétrage quelconque.
|
|




suivant: 7.2.0.2 Portion régulière de
monter: 7.2 Paramétrage - Portion
précédent: 7.2 Paramétrage - Portion
Table des matières
2002-12-17
![]() de
de
![]() , les trois composantes
, les trois composantes
![]() ,
, ![]() , de
, de ![]() sont des fonctions de classe
sont des fonctions de classe ![]() et la condition sur
et la condition sur ![]() signifie très exactement que les vecteurs
signifie très exactement que les vecteurs