



suivant: 7.5 Les formes fondamentales
monter: 7.4 Plan tangent, orientation
précédent: 7.4.0.1 Plan tangent
Table des matières
Pour orienter le plan tangent 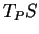 , il suffit d'en choisir une
normale unitaire
, il suffit d'en choisir une
normale unitaire 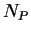 , les bases positives
, les bases positives
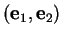 de
de
 étant alors celles pour lesquelles
étant alors celles pour lesquelles
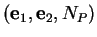 est une base positive de
est une base positive de
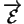 .
.
Un paramétrage
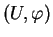 permet d'orienter les plans tangents à
permet d'orienter les plans tangents à
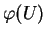 grâce à la normale unitaire
grâce à la normale unitaire
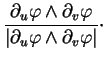 |
(7.6) |
De même, une équation cartésienne 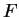 donne une normale unitaire
privilégiée
donne une normale unitaire
privilégiée
On dit que la surface  est orientée lorsqu'on a choisi une
normale unitaire
est orientée lorsqu'on a choisi une
normale unitaire
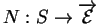 qui dépende continûment de
qui dépende continûment de
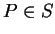 , c'est-à-dire telle que, pour tout paramétrage
, c'est-à-dire telle que, pour tout paramétrage
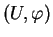 ,
,
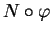 soit continu. Comme il n'y a que deux normales
unitaires possibles en chaque point, un tel choix coïncide forcément
avec (37) ou avec son opposé. En conséquence,
soit continu. Comme il n'y a que deux normales
unitaires possibles en chaque point, un tel choix coïncide forcément
avec (37) ou avec son opposé. En conséquence,
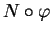 est une fonction de classe
est une fonction de classe 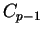 . Dans la suite, nous désignerons
par
. Dans la suite, nous désignerons
par
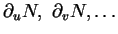 les dérivées partielles de
les dérivées partielles de
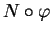 par rapport aux paramètres
par rapport aux paramètres
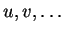 Bien
entendu, on peut aussi orienter
Bien
entendu, on peut aussi orienter  avec la normale associée à une
équation cartésienne.
avec la normale associée à une
équation cartésienne.
Figure 10:
Un ruban de Moebius.
|
|
Remarque 7.4.3
Les surfaces plus générales dont il est question dans la note
en bas de page (
1) ne sont pas toujours orientables. L'
exemple du
Ruban de Moebius est sans doute un des plus
célèbres. Une surface non orientable n'a pas deux faces mais
seulement une: il n'y a ni ``au-dessus" ni ``en-dessous". Dans le
cas du Ruban de Moebius, cette particularité est exploitée pour
répartir de façon homogène l'usure des courroies de transmission.
Remarque 7.4.4
En chaque point

de

, orienté par la normale
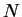
, on
obtient une base
de
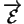
. C'est l'analogue pour les surfaces du trièdre de Frenet des courbes.




suivant: 7.5 Les formes fondamentales
monter: 7.4 Plan tangent, orientation
précédent: 7.4.0.1 Plan tangent
Table des matières
2002-12-17
![]() , il suffit d'en choisir une
normale unitaire
, il suffit d'en choisir une
normale unitaire ![]() , les bases positives
, les bases positives
![]() de
de
![]() étant alors celles pour lesquelles
étant alors celles pour lesquelles
![]() est une base positive de
est une base positive de
![]() .
.
![]() permet d'orienter les plans tangents à
permet d'orienter les plans tangents à
![]() grâce à la normale unitaire
grâce à la normale unitaire
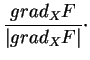
![]() est orientée lorsqu'on a choisi une
normale unitaire
est orientée lorsqu'on a choisi une
normale unitaire
![]() qui dépende continûment de
qui dépende continûment de
![]() , c'est-à-dire telle que, pour tout paramétrage
, c'est-à-dire telle que, pour tout paramétrage
![]() ,
,
![]() soit continu. Comme il n'y a que deux normales
unitaires possibles en chaque point, un tel choix coïncide forcément
avec (37) ou avec son opposé. En conséquence,
soit continu. Comme il n'y a que deux normales
unitaires possibles en chaque point, un tel choix coïncide forcément
avec (37) ou avec son opposé. En conséquence,
![]() est une fonction de classe
est une fonction de classe ![]() . Dans la suite, nous désignerons
par
. Dans la suite, nous désignerons
par
![]() les dérivées partielles de
les dérivées partielles de
![]() par rapport aux paramètres
par rapport aux paramètres
![]() Bien
entendu, on peut aussi orienter
Bien
entendu, on peut aussi orienter ![]() avec la normale associée à une
équation cartésienne.
avec la normale associée à une
équation cartésienne.