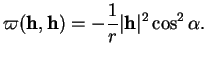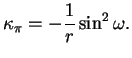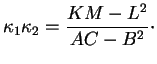suivant: 7.7 Les surfaces du
monter: 7 Surfaces
précédent: 7.5.3 Le théorème de
Table des matières
Le lemme suivant montre que les sections d'une surface par des plans
normaux sont, localement, des arcs réguliers de courbes.
Lemme 7.6.1
L'intersection
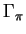
de
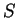
avec un plan
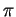
contenant la
droite
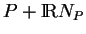
est, au voisinage de

, un arc régulier de
courbe.
Preuve. Notons
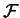 la restriction à
la restriction à 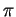 d'une équation cartésienne
d'une équation cartésienne
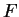 de
de 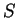 . Si
. Si
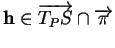 n'est pas nul,
alors
n'est pas nul,
alors
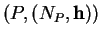 est un repère de
est un repère de 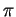 et l'expression de
et l'expression de
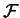 dans les coordonnées
dans les coordonnées
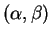 correspondantes est
Les dérivées partielles de cette fonction en
correspondantes est
Les dérivées partielles de cette fonction en 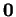 sont donc
car
sont donc
car 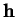 est perpendiculaire à
est perpendiculaire à 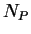 . Elles ne sont pas nulles. Par
conséquent,
. Elles ne sont pas nulles. Par
conséquent,
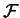 est une équation cartésienne de
est une équation cartésienne de
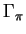 au
voisinage de
au
voisinage de  .
.
Figure:
Signe de
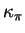 et concavité de la section par un plan normal
et concavité de la section par un plan normal 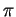 .
.
|
|
Soient un plan 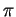 normal à
normal à 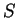 en
en  , c'est-à-dire
contenant
, c'est-à-dire
contenant
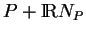 , et
, et
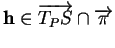 , non
nul. Le rapport
, non
nul. Le rapport
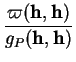 |
(7.8) |
ne change pas lorsqu'on remplace 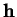 par un quelconque de ses
multiples non nuls, par exemple par une tangente unitaire à
par un quelconque de ses
multiples non nuls, par exemple par une tangente unitaire à
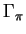 . D'après le théorème de Meusnier, c'est donc la
courbure de
. D'après le théorème de Meusnier, c'est donc la
courbure de
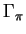 en
en  si
si 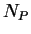 est orienté vers la
concavité de
est orienté vers la
concavité de
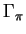 et son opposé sinon. On le note
et son opposé sinon. On le note
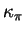 . On l'appelle la courbure normale de
. On l'appelle la courbure normale de 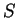 en
en  associée à
associée à 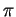 .
.
Théorème 7.6.2
Lorsque
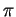
décrit les plans normaux à
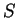
en

,
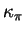
atteint un minimum
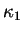
et un maximum
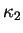
.
Si
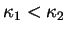
, ils sont associés à des plans orthogonaux.
Les valeurs extrêmes
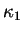
et
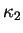
sont les racines de
l'équation en
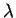
Preuve. Les valeurs de (39) sont entièrement déterminées par
sa restriction aux 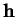 de longueur
de longueur 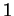 . Il atteint donc un minimum
et un maximum absolus en de tels
. Il atteint donc un minimum
et un maximum absolus en de tels 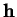 car ceux-ci forment un compact
sur lequel il est continu.
car ceux-ci forment un compact
sur lequel il est continu.
On peut détecter ces valeurs extrêmes par la règle des multiplicateurs
de Lagrange. Quand (39) est évalué en un vecteur de
longueur 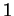 , il se réduit à
, il se réduit à
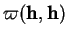 . Les
. Les 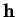 stationnaires de (39) sous la contrainte
stationnaires de (39) sous la contrainte
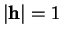 sont donc ceux pour lesquels il existe
sont donc ceux pour lesquels il existe
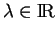 tel que
tel que
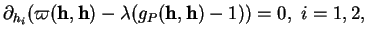 |
(7.9) |
où
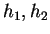 sont les composantes de
sont les composantes de 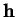 dans une base
quelconque de
dans une base
quelconque de
 .
.
Prenons d'abord une base orthonormée. Cela donne les équations
auxquelles il faut ajouter la condition
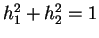 . En
multipliant la première par
. En
multipliant la première par 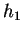 , la seconde par
, la seconde par 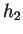 puis en les
additionnant, on constate que
puis en les
additionnant, on constate que
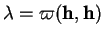 . De plus,
elles signifient que le vecteur
. De plus,
elles signifient que le vecteur
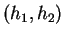 est un vecteur propre de valeur propre
est un vecteur propre de valeur propre
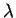 de la matrice
Comme elle est symétrique, ses valeurs propres sont réelles et ses
vecteurs propres relatifs à des valeurs propres distinctes sont
orthogonaux. Ceci démontre la première partie de l'énoncé.
de la matrice
Comme elle est symétrique, ses valeurs propres sont réelles et ses
vecteurs propres relatifs à des valeurs propres distinctes sont
orthogonaux. Ceci démontre la première partie de l'énoncé.
Le même calcul dans la base
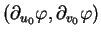 donne la forme
donne la forme
aux équations (40).
Pour que ce système admette une solution non nulle, il faut et il
suffit que 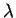 annule le déterminant de la matrice des
coefficients des inconnues. D'où le théorème.
annule le déterminant de la matrice des
coefficients des inconnues. D'où le théorème.
Remarque 7.6.3
Il résulte de la démonstration précédente que les valeurs
extrêmes de
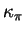
et les directions tangentes associées
sont les valeurs propres et les vecteurs propres
de l'application de
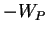
.
Les nombres
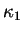 et
et
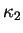 sont les courbures
principales de
sont les courbures
principales de 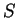 en
en  . Quand ils sont distincts, ils sont associés
à des plans normaux perpendiculaires qui coupent le plan
. Quand ils sont distincts, ils sont associés
à des plans normaux perpendiculaires qui coupent le plan 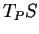 selon deux tangentes à
selon deux tangentes à 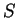 dont les directions sont les directions principales de
dont les directions sont les directions principales de 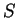 en
en  .
.
Lorsque
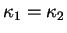 , toutes les courbures normales de
, toutes les courbures normales de 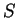 en
en  sont égales. Le point
sont égales. Le point  s'appelle alors un ombilic. Il
est plat si
s'appelle alors un ombilic. Il
est plat si
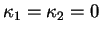 . Les points d'une sphère
sont tous des ombilics, non plats.
. Les points d'une sphère
sont tous des ombilics, non plats.
Lorsque
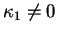 ou
ou
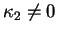 , alors
, alors  est elliptique,
parabolique ou hyperbolique selon que, respectivement,
est elliptique,
parabolique ou hyperbolique selon que, respectivement,
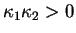 ,
,
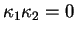 ou
ou
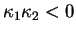 .
.
Le produit
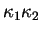 est la courbure de Gauss de
est la courbure de Gauss de
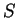 en
en  . La somme
. La somme
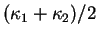 est sa courbure
moyenne.
est sa courbure
moyenne.
Les points d'un cylindre circulaire droit sont tous paraboliques. Si
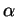 est l'angle non orienté que fait en
est l'angle non orienté que fait en  la tangente de vecteur-directeur
la tangente de vecteur-directeur 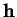 avec la tangente orthogonale aux génératrices, on a vu plus haut que
avec la tangente orthogonale aux génératrices, on a vu plus haut que
Par conséquent, la courbure normale associée à un plan normal 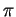 faisant un angle
faisant un angle 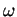 avec les génératrices vaut
Elle atteint son minimum
avec les génératrices vaut
Elle atteint son minimum
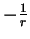 lorsque
lorsque 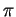 est orthogonal aux génératrices et
son maximum 0 lorsqu'il leur est parallèle. Les directions
principales en un point sont donc celles de la génératrice passant
par ce point et de la tangente qui lui est perpendiculaire.
est orthogonal aux génératrices et
son maximum 0 lorsqu'il leur est parallèle. Les directions
principales en un point sont donc celles de la génératrice passant
par ce point et de la tangente qui lui est perpendiculaire.
En général, la courbure de Gauss est donnée par
Remarque 7.6.4
L'application de Weingarten et la seconde forme fondamentale
dépendent de l'orientation de
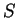
. Quand on remplace
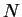
par
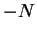
,
elles sont remplacées par leurs opposés. Les courbures normales
sont également remplacées par leurs opposés, de même que la
courbure moyenne. La courbure de Gauss
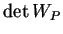
est par
contre indépendante de l'orientation.




suivant: 7.7 Les surfaces du
monter: 7 Surfaces
précédent: 7.5.3 Le théorème de
Table des matières
2002-12-17
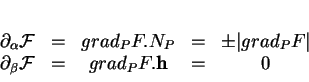
![]() normal à
normal à ![]() en
en ![]() , c'est-à-dire
contenant
, c'est-à-dire
contenant
![]() , et
, et
![]() , non
nul. Le rapport
, non
nul. Le rapport
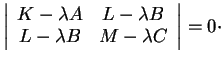
![]() , il se réduit à
, il se réduit à
![]() . Les
. Les ![]() stationnaires de (39) sous la contrainte
stationnaires de (39) sous la contrainte
![]() sont donc ceux pour lesquels il existe
sont donc ceux pour lesquels il existe
![]() tel que
tel que
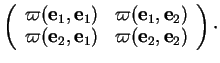
![]() donne la forme
donne la forme
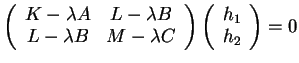
![]() et
et
![]() sont les courbures
principales de
sont les courbures
principales de ![]() en
en ![]() . Quand ils sont distincts, ils sont associés
à des plans normaux perpendiculaires qui coupent le plan
. Quand ils sont distincts, ils sont associés
à des plans normaux perpendiculaires qui coupent le plan ![]() selon deux tangentes à
selon deux tangentes à ![]() dont les directions sont les directions principales de
dont les directions sont les directions principales de ![]() en
en ![]() .
.
![]() , toutes les courbures normales de
, toutes les courbures normales de ![]() en
en ![]() sont égales. Le point
sont égales. Le point ![]() s'appelle alors un ombilic. Il
est plat si
s'appelle alors un ombilic. Il
est plat si
![]() . Les points d'une sphère
sont tous des ombilics, non plats.
. Les points d'une sphère
sont tous des ombilics, non plats.
![]() ou
ou
![]() , alors
, alors ![]() est elliptique,
parabolique ou hyperbolique selon que, respectivement,
est elliptique,
parabolique ou hyperbolique selon que, respectivement,
![]() ,
,
![]() ou
ou
![]() .
.
![]() est la courbure de Gauss de
est la courbure de Gauss de
![]() en
en ![]() . La somme
. La somme
![]() est sa courbure
moyenne.
est sa courbure
moyenne.
![]() est l'angle non orienté que fait en
est l'angle non orienté que fait en ![]() la tangente de vecteur-directeur
la tangente de vecteur-directeur ![]() avec la tangente orthogonale aux génératrices, on a vu plus haut que
avec la tangente orthogonale aux génératrices, on a vu plus haut que