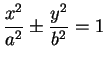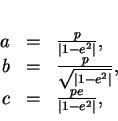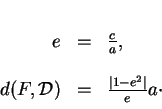suivant: 6.4.3.1.1 Equation polaire
monter: 6.4.3 Les courbes du
précédent: 6.4.3 Les courbes du
Table des matières
L'ellipse, la parabole et l'hyperbole sont étudiées à l'école secondaire. En voici une présentation rapide et unifiée, basée sur les notions de directrice,
foyer et excentricité qui s'avère très utile dans l'étude du problème des deux corps, et en particulier dans la description du mouvement des
planètes.
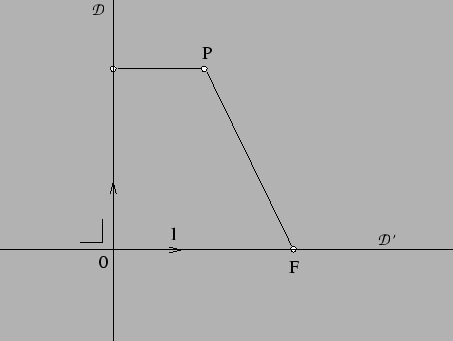
Figure:
Coniques définies par foyer et directrice.
|
|
Proposition 6.4.6
Soient une droite

, un point
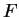
non situé sur

et un nombre positif
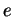
. Le lieu des points

de

tels que
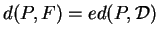
est une conique dont
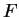
est un foyer et dont la perpendiculaire à

issue de
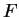
est un axe de symétrie. C'est une ellipse, une parabole ou une hyperbole selon que
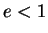
,
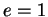
ou
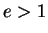
respectivement.
Preuve. Soit 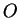 le point de percée de la perpendiculaire
le point de percée de la perpendiculaire
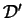 abaissée de
abaissée de 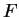 sur
sur
 ,
, 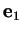 un vecteur-directeur normé de
un vecteur-directeur normé de
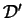 orienté de
orienté de 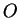 vers
vers 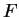 , et
, et
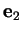 un vecteur-directeur normé de
un vecteur-directeur normé de
 formant avec
formant avec 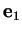 une base positive. Dans le repère
une base positive. Dans le repère
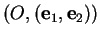 , l'équation du lieu est
où
, l'équation du lieu est
où 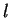 est la distance de
est la distance de 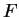 à
à
 . Après élévation des deux membres au carré et transformations, on obtient l'équation équivalente
. Après élévation des deux membres au carré et transformations, on obtient l'équation équivalente
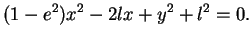 |
(6.6) |
Si 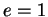 , le lieu est par définition une parabole de directrice
, le lieu est par définition une parabole de directrice
 et de foyer
et de foyer  . Ceci est confirmé par la forme familière
. Ceci est confirmé par la forme familière
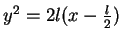 à laquelle se réduit alors l'équation ci-dessus(6.11).
Lorsque
à laquelle se réduit alors l'équation ci-dessus(6.11).
Lorsque 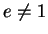 , l'équation (28) peut se réécrire en
La conclusion est alors évidente.
, l'équation (28) peut se réécrire en
La conclusion est alors évidente.
La droite
 s'appelle la directrice de foyer
s'appelle la directrice de foyer 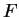 et
et 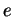 est l'excentricité.
est l'excentricité.
Lorsque 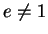 , on ramène aisément l'équation précédente du lieu à la forme canonique:
, on ramène aisément l'équation précédente du lieu à la forme canonique:
en translatant l'origine du repère en le point de coordonnées
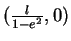 . Le demi ``grand axe"
. Le demi ``grand axe" 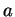 , le
demi ``petit axe"
, le
demi ``petit axe" 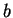 et la moitié
et la moitié 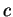 de la distance entre les foyers sont alors donnés par les formules
où
de la distance entre les foyers sont alors donnés par les formules
où 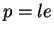 . On remarque aussi que
En particulier, lorsque
. On remarque aussi que
En particulier, lorsque 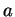 est constant mais que
est constant mais que 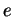 devient de plus en plus petit,
devient de plus en plus petit,
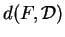 grandit de plus en plus tandis que
grandit de plus en plus tandis que 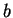 se rapproche de
se rapproche de 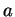 .
Cela fait dire que les cercles sont des ellipses d'excentricité nulle dont
la directrice est ``rejetée à l'infini".
.
Cela fait dire que les cercles sont des ellipses d'excentricité nulle dont
la directrice est ``rejetée à l'infini".
Sous-sections




suivant: 6.4.3.1.1 Equation polaire
monter: 6.4.3 Les courbes du
précédent: 6.4.3 Les courbes du
Table des matières
2002-12-17
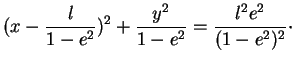
![]() s'appelle la directrice de foyer
s'appelle la directrice de foyer ![]() et
et ![]() est l'excentricité.
est l'excentricité.
![]() , on ramène aisément l'équation précédente du lieu à la forme canonique:
, on ramène aisément l'équation précédente du lieu à la forme canonique: