suivant: 2 Géométrie affine
monter: 1.5 Sous-espaces vectoriels
précédent: 1.5.5 Cas de la
Table des matières
1.5.6 Cas de la dimension 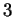
Lorsque  est de dimension
est de dimension 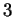 , en dehors de
, en dehors de  et de
et de 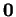 , les sous-espaces vectoriels sont de dimension
, les sous-espaces vectoriels sont de dimension 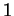 ou
ou 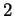 .
Dans une base
.
Dans une base
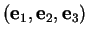 de
de  , une droite vectorielle
, une droite vectorielle 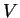 est caractérisée par deux équations homogènes du premier degré indépendantes
est caractérisée par deux équations homogènes du premier degré indépendantes
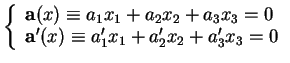 |
(1.8) |
L'indépendance des équations se traduit par le fait que
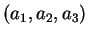 n'est pas multiple de
n'est pas multiple de
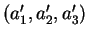 et inversement.
Les équations (8) admettent la solution
formée des mineurs algébriques extraits du tableau des coefficients
Ils ne sont pas nuls, sinon
et les équations ne seraient pas indépendantes. Ces mineurs sont donc les composantes d'une base de
et inversement.
Les équations (8) admettent la solution
formée des mineurs algébriques extraits du tableau des coefficients
Ils ne sont pas nuls, sinon
et les équations ne seraient pas indépendantes. Ces mineurs sont donc les composantes d'une base de 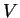 qui admet ainsi les équations paramétriques
qui admet ainsi les équations paramétriques
Les plans vectoriels sont des hyperplans. Ils sont donc décrits par une équations cartésienne non nulle déterminée à un multiple non nul près.
Proposition 1.5.12
Dans un espace vectoriel de dimension
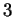
, deux plans vectoriels distincts se coupent selon une droite vectorielle.
Preuve. En effet, deux plans distincts sont caractérisés par des équations cartésiennes indépendantes.
Proposition 1.5.13
Dans un espace vectoriel de dimension
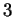
, un plan vectoriel contient une droite vectorielle d'équations cartésiennes (
8)
si et seulement si il admet une équation cartésienne de la forme
où
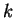
et
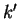
ne sont pas tous les deux nuls.
Figure 2:
Les plans vectoriels contenant une droite vectorielle.
|
|
Preuve. Le sous-espace vectoriel d'équation cartésienne
contient la droite vectorielle 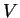 d'équation (8) si et seulement si
Comme
d'équation (8) si et seulement si
Comme
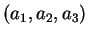 et
et
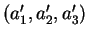 forment une base de
forment une base de
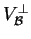 ,
ceci équivaut à ce que
,
ceci équivaut à ce que
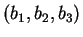 soit combinaison linéaire de ces derniers, à coefficients non tous nuls.
soit combinaison linéaire de ces derniers, à coefficients non tous nuls.
Corollaire 1.5.14
Dans un espace vectoriel de dimension
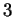
, trois plans vectoriels deux à deux distincts d'équations cartésiennes
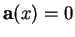
,
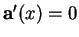
,
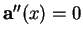
se coupent selon un droite vectorielle si et seulement si leurs équations sont linéairement dépendantes:
pour certains
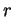
,
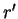
,
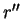
non tous nuls.
Preuve. En effet, l'équation de l'un de ces plans est combinaison de celles des deux autres puisqu'il contient la droite vectorielle intersection de ceux-ci.
Remarque 1.5.15
Traditionnellement, en dimension
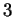
, les composantes sont notées
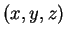
plutôt que
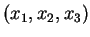
.
Remarque 1.5.16
On peut établir qu'il existe des équations paramétriques
canoniques uniquement:
- pour les droites vectorielles quelque soit la dimension de

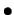
- pour les hyperplans vectoriels en dimensions
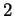 ,
, 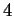 et
et 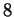 .
.
En dimension quelconque, les mineurs algébriques du tableau des coefficients des équations cartésiennes d'une droite
forment une base de celle-ci, d'où découlent comme indiqué plus haut en dimensions 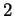 et
et 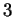 ,
des équations paramétriques canoniques des droites vectorielles.
En dimensions
,
des équations paramétriques canoniques des droites vectorielles.
En dimensions 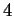 , les vecteurs de composantes
, les vecteurs de composantes
forment une base de l'hyperplan d'équation
Des formules analogues existent pour décrire les sept éléments d'une base d'un hyperplan en dimension
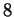
.
Nous ne les donnerons pas ici.
La démonstration du fait que ces cas soient les seuls pour lesquels il existe des formules générales est très difficile!




suivant: 2 Géométrie affine
monter: 1.5 Sous-espaces vectoriels
précédent: 1.5.5 Cas de la
Table des matières
2002-12-17
![]() est de dimension
est de dimension ![]() , en dehors de
, en dehors de ![]() et de
et de ![]() , les sous-espaces vectoriels sont de dimension
, les sous-espaces vectoriels sont de dimension ![]() ou
ou ![]() .
Dans une base
.
Dans une base
![]() de
de ![]() , une droite vectorielle
, une droite vectorielle ![]() est caractérisée par deux équations homogènes du premier degré indépendantes
est caractérisée par deux équations homogènes du premier degré indépendantes
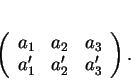
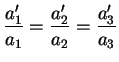
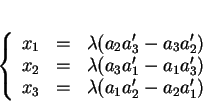
![]() et
et ![]() ,
des équations paramétriques canoniques des droites vectorielles.
En dimensions
,
des équations paramétriques canoniques des droites vectorielles.
En dimensions ![]() , les vecteurs de composantes
, les vecteurs de composantes