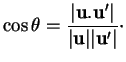L'angle ![]() de deux droites
de deux droites
![]() et
et
![]() est le plus petit des angles non orientés
est le plus petit des angles non orientés ![]() que font un vecteur-directeur
que font un vecteur-directeur ![]() de l'une et un
vecteur-directeur
de l'une et un
vecteur-directeur
![]() de l'autre. Comme
de l'autre. Comme
![]() ne change éventuellement que de signe pour un autre choix de
ne change éventuellement que de signe pour un autre choix de ![]() et
et ![]() ,
,
![]() est compris entre 0 et
est compris entre 0 et
![]() et est donné par la formule
et est donné par la formule