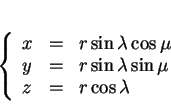Une origine
![]() étant fixée, un point
étant fixée, un point ![]() est complètement caractérisé par la distance
est complètement caractérisé par la distance ![]() et la position du point que le rayon-vecteur
et la position du point que le rayon-vecteur
![]() découpe sur la sphère de centre
découpe sur la sphère de centre ![]() et de rayon
et de rayon ![]() . On obtient ainsi d'autres manières de décrire les éléments de
. On obtient ainsi d'autres manières de décrire les éléments de
![]() par des nombres qu'en utilisant
un repère orthonormé. Ces systèmes de coodonnées alternatifs sont mieux adaptés à certains problèmes que les coordonées cartésiennes.
par des nombres qu'en utilisant
un repère orthonormé. Ces systèmes de coodonnées alternatifs sont mieux adaptés à certains problèmes que les coordonées cartésiennes.
Supposons d'abord
![]() de dimension
de dimension ![]() , et orienté.
La position d'un point
, et orienté.
La position d'un point ![]() sur le cercle de centre
sur le cercle de centre ![]() et de rayon
et de rayon ![]() est entièrement caractérisée par l'angle orienté
est entièrement caractérisée par l'angle orienté ![]() que fait
que fait
![]() avec un
vecteur normé de référence
avec un
vecteur normé de référence
![]() donné. Les nombres
donné. Les nombres ![]() et
et ![]() sont les coordonées polaires du point
sont les coordonées polaires du point ![]() . Par définition, on a
. Par définition, on a ![]() ,
,
![]() . De plus, les coordonnées
. De plus, les coordonnées ![]() de
de ![]() dans le repère orthonormé positif
dans le repère orthonormé positif
![]() sont données par
sont données par
Supposons à présent
![]() de dimension
de dimension ![]() et, à nouveau, orienté. Pour caractériser la position d'un point sur la sphère
et, à nouveau, orienté. Pour caractériser la position d'un point sur la sphère ![]() , on utilise un repère orthonormé
positif
, on utilise un repère orthonormé
positif
![]() (les indices sont choisis pour rappeler les noms
(les indices sont choisis pour rappeler les noms ![]() ,
, ![]() et
et ![]() adoptés pour les coordonnées). Un point
adoptés pour les coordonnées). Un point ![]() de la sphère, non
situé sur l'axe
de la sphère, non
situé sur l'axe ![]() (
(
![]() ) forme avec celui-ci un plan
) forme avec celui-ci un plan ![]() qui coupe la sphère selon un cercle (le méridien auquel appartient
qui coupe la sphère selon un cercle (le méridien auquel appartient ![]() ). Deux angles
suffisent alors: un pour localiser
). Deux angles
suffisent alors: un pour localiser ![]() sur son méridien (la latitude), l'autre pour selectionner celui-ci, c'est-à-dire caractériser
sur son méridien (la latitude), l'autre pour selectionner celui-ci, c'est-à-dire caractériser ![]() parmi tous les
plans passant par
parmi tous les
plans passant par ![]() (la longitude). Un choix usuel consiste à prendre pour latitude(4.6) l'angle non orienté
(la longitude). Un choix usuel consiste à prendre pour latitude(4.6) l'angle non orienté ![]() entre
entre ![]() et
et
![]() , et pour longitude, l'angle orienté
, et pour longitude, l'angle orienté ![]() formé
par
formé
par ![]() et
et
![]() , où
, où ![]() est la projection orthogonale de
est la projection orthogonale de ![]() sur le plan formé par les axes
sur le plan formé par les axes ![]() et
et ![]() etñ orienté par le repère
etñ orienté par le repère
![]() .
.
Les coordonées sphériques d'un point
![]() sont alors les nombres
sont alors les nombres
![]() . On a
. On a ![]() ,
,
![]() et
et
![]() . De plus, elles sont liées aux coordonnées cartésiennes de
. De plus, elles sont liées aux coordonnées cartésiennes de ![]() dans le repère
dans le repère
![]() par les formules
par les formules