



suivant: 2.2.2 Exemple
monter: 2.2 Espaces affines
précédent: 2.2 Espaces affines
Table des matières
Un espace affine (modelé) sur un espace vectoriel  est la donnée d'un ensemble
est la donnée d'un ensemble
 dont les éléments sont appelés points et, pour chaque
dont les éléments sont appelés points et, pour chaque
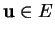 , d'une application
, d'une application
appelée translation de vecteur 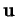 , tels que
, tels que
- (a)
- Si
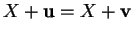 pour au moins un
pour au moins un
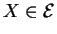 , alors
, alors
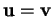 .
.
- (b)
- Quels que soient les éléments
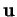 et
et 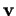 de
de  , la composée des translations de vecteurs
, la composée des translations de vecteurs 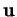 et
et 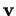 est la translation de vecteur
est la translation de vecteur
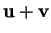 :
:
Figure 1:
Pour composer des translations, on additionne leurs vecteurs.
|
|
- (c)
- La translation de vecteur
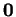 est l'identité:
est l'identité:
- (d)
- Quels que soient les points
 et
et 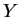 de
de
 , il existe un élément
, il existe un élément
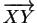 de
de  tel que
tel que
Figure 2:
La translation de vecteur
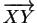 est la seule transformant
est la seule transformant  en
en 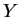 .
.
|
|
Remarque 2.2.1
Vu (a),
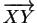
est le seul
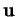
tel que
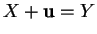
.
Proposition 2.2.2
Les translations sont des bijections. L'inverse de la translation de vecteur
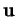
est celle de vecteur
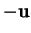
.
Preuve. En effet, vu (b) et (c),
est l'identité. 
Proposition 2.2.3
Trois points quelconques

,
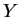
et
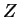
de

vérifient toujours la
relation de Chasles
En particulier,
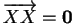
et
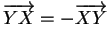
.
Preuve. On a, en appliquant répétitivement (b) et (d),
Comme 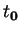 , la translation de vecteur
, la translation de vecteur
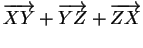 transforme donc
transforme donc  en
en  . D'après (a), il en résulte que ce dernier est nul.
. D'après (a), il en résulte que ce dernier est nul.
On obtient
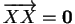 en faisant
en faisant 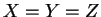 dans la relation de Chasles. Il vient ensuite
dans la relation de Chasles. Il vient ensuite
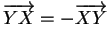 en y faisant
en y faisant 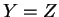 .
.
Figure:
La relation de Chasles: trois points déterminent au plus deux directions indépendantes.
|
|
Remarque 2.2.4
La relation de Chasles prend la forme très utile
permettant d'exprimer
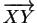
à l'aide d'un point
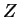
quelconque, ce qui conduit d'ailleurs à écrire
En général, l'espace vectoriel  sous-jacent à
sous-jacent à
 est spécifié par le contexte. Il arrive que l'on doive le désigner explicitement, auquel cas nous le
représenterons par
est spécifié par le contexte. Il arrive que l'on doive le désigner explicitement, auquel cas nous le
représenterons par
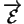 .
.




suivant: 2.2.2 Exemple
monter: 2.2 Espaces affines
précédent: 2.2 Espaces affines
Table des matières
2002-12-17
![]() est la donnée d'un ensemble
est la donnée d'un ensemble
![]() dont les éléments sont appelés points et, pour chaque
dont les éléments sont appelés points et, pour chaque
![]() , d'une application
, d'une application
![]() en faisant
en faisant ![]() dans la relation de Chasles. Il vient ensuite
dans la relation de Chasles. Il vient ensuite
![]() en y faisant
en y faisant ![]() .
.![]()
![]() sous-jacent à
sous-jacent à
![]() est spécifié par le contexte. Il arrive que l'on doive le désigner explicitement, auquel cas nous le
représenterons par
est spécifié par le contexte. Il arrive que l'on doive le désigner explicitement, auquel cas nous le
représenterons par
![]() .
.