



suivant: 5.3.2.2 Rotations spatiales
monter: 5.3.2 Rotations
précédent: 5.3.2 Rotations
Table des matières
Supposons à présent que
 soit de dimension
soit de dimension 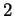 .
.
Proposition 5.3.4
Soit une rotation
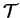
de

admettant le point fixe
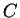
.
(i) L'angle orienté
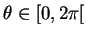 entre
entre 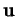 et
et
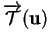 est indépendant de
est indépendant de
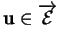 .
.
(ii) Dans tout repère orthonormé positif d'origine 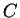 de
de
 ,
,
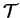 est représenté par l'application
est représenté par l'application
Figure 8:
Rotation plane d'angle 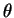 et centre
et centre 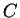 .
.
|
|
Preuve. Dans un repère orthonormé positif d'origine 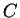 ,
,
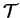 est représenté sous la forme (22) où
est représenté sous la forme (22) où
est orthogonale et de déterminant 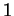 . Les colonnes étant normées et orthogonales,
. Les colonnes étant normées et orthogonales, 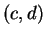 ne peut que valoir
ne peut que valoir 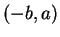 ou
ou 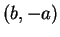 .
Il vaut
.
Il vaut 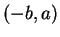 car le déterminant de
car le déterminant de  est positif. Cela étant, puisque
est positif. Cela étant, puisque 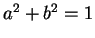 , il existe un seul nombre
, il existe un seul nombre
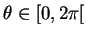 tel que
tel que
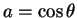 et
et
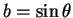 . La matrice
. La matrice 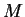 est donc de la forme prévue dans (ii). Pour terminer la démonstration, il suffit de montrer que
est donc de la forme prévue dans (ii). Pour terminer la démonstration, il suffit de montrer que 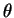 à la
propriété indiquée dans (i). Si
à la
propriété indiquée dans (i). Si 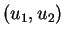 sont les composantes de
sont les composantes de
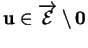 , celles de
, celles de
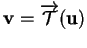 sont
De là,
et
D'où la conclusion.
sont
De là,
et
D'où la conclusion.
L'angle orienté 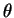 dont il est question en
dont il est question en 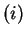 est l'amplitude de la rotation
est l'amplitude de la rotation
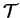 (5.5). On désigne par
(5.5). On désigne par
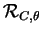 la rotation de point fixe
la rotation de point fixe 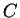 et d'amplitude
et d'amplitude 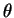 .
Un calcul élémentaire montre que
.
Un calcul élémentaire montre que
La rotation
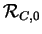 est l'identité
est l'identité
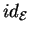 . C'est la seule rotation plane ayant plus d'un point fixe.
La rotation
. C'est la seule rotation plane ayant plus d'un point fixe.
La rotation
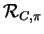 est la symétrie centrale par rapport à
est la symétrie centrale par rapport à  .
.




suivant: 5.3.2.2 Rotations spatiales
monter: 5.3.2 Rotations
précédent: 5.3.2 Rotations
Table des matières
2002-12-17
![]() soit de dimension
soit de dimension ![]() .
.
![]() entre
entre ![]() et
et
![]() est indépendant de
est indépendant de
![]() .
.
![]() de
de
![]() ,
,
![]() est représenté par l'application
est représenté par l'application
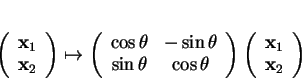
![]() ,
,
![]() est représenté sous la forme (22) où
est représenté sous la forme (22) où
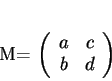
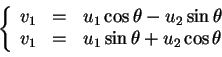
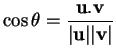
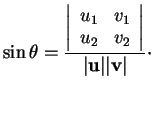
![]() dont il est question en
dont il est question en ![]() est l'amplitude de la rotation
est l'amplitude de la rotation
![]() (5.5). On désigne par
(5.5). On désigne par
![]() la rotation de point fixe
la rotation de point fixe ![]() et d'amplitude
et d'amplitude ![]() .
Un calcul élémentaire montre que
.
Un calcul élémentaire montre que