suivant: 7.5.2.1 Expression de
monter: 7.5 Les formes fondamentales
précédent: 7.5.1.0.2 L'élément de surface
Table des matières
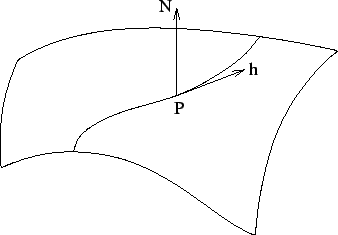
Figure:
Dériver 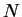 dans la direction de
dans la direction de 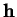 : application de Weingarten.
: application de Weingarten.
|
|
Pour étudier la courbure de  au voisinage de
au voisinage de  , l'idée est
d'examiner la manière dont la normale
, l'idée est
d'examiner la manière dont la normale 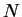 varie aux alentours de
varie aux alentours de  .
En particulier, on peut dériver
.
En particulier, on peut dériver 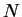 dans la direction de chaque
vecteur tangent à
dans la direction de chaque
vecteur tangent à  en
en  . Comme
. Comme 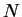 est de longueur constante
est de longueur constante
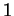 , ces dérivées lui sont orthogonales. Elles sont donc tangentes à
, ces dérivées lui sont orthogonales. Elles sont donc tangentes à
 en
en  . L'application qui transforme
. L'application qui transforme
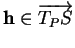 en la
dérivée
en la
dérivée
 de
de  dans la direction de
dans la direction de 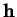 est l'application de Weingarten de
est l'application de Weingarten de  en
en  . La seconde
forme fondamentale de
. La seconde
forme fondamentale de  en
en  est alors, par définition,
est alors, par définition,
Sous-sections
2002-12-17