7.7.0.1.2 Conclusions

Avec ces remarques, on voit que l'on est ramené à l'un des cas suivants.

• $(\alpha_{1}\alpha_{2}\alpha_{3}\neq 0)$
  

  $$x_{1}^{2} + x_{2}^{2}\pm x_{3}^{2} + \gamma =$$ 0

  
  

• $(\alpha_{1}\alpha_{2}\neq 0,\ \alpha_{3}=0)$
  

  $$x_{1}^{2} \pm x_{2}^{2} + 2\beta x_{3} = 0 \ (\beta \neq 0)$$

  $$x_{1}^{2} \pm x_{2}^{2} + \gamma =$$ 0

  
  

• $(\alpha_{1}\neq 0, \ \alpha_{2}=\alpha_{3}=0)$
  

  $$x_{1}^{2} + 2\beta x_{2} = 0 \ (\beta \neq 0)$$

  $$x_{1}^{2} + \gamma = 0.$$

  
  

Une équation dans laquelle manque une variable représente un cylindre. Si $x_{i}$ manque, l'ensemble décrit par l'équation contient en effet les droites parallèles à ${\bf e}_{i}$ qui passent par ses points. La section du cylindre par un plan orthogonal à ${\bf e}_{i}$ est une conique. C'est un cylindre elliptique, parabolique ou hyperbolique selon que cette conique est une ellipse, une parabole ou une hyperbole proprement dite. L'équation en est alors une équation cartésienne. Elle peut également être vide ou dégénérée. Dans ce dernier cas, le cylindre est fait de deux plans (sécants ou parallèles, voire confondus) ou est réduit à une droite.

Lorsque l'équation est homogène, elle représente un cône (cela arrive exactement quand $\beta$ et $\gamma$ sont nuls). L'ensemble décrit par l'équation contient en effet alors les droites qui passent par l'origine du repère et par un quelconque de ses points, distincts de celle-ci. Il peut être réduit à un point (lorsque les trois $\alpha_{i}$ sont non nuls et de même signe). Il peut être dégénéré (lorsqu'un $\alpha_{i}$ est nul) et consister en un ou deux plans ou en une droite.

Lorsque les $\alpha_{i}$ sont de même signe que $\gamma$, l'équation n'a pas de solution et l'ensemble qu'elle décrit est vide.

Dans tous les autres cas, l'équation décrit une surface dont elle est une équation cartésienne, une quadrique. Voici la nomenclature, et les équations canoniques dans un repère orthonormé (on y désigne plus classiquement les coordonnées par $x$, $y$ et $z$).

a)Ellipsoïde ($E$) Il s'agit du cas où $\alpha_{1}, \alpha_{2}, \alpha_{3}$ sont de même signe, opposé à celui de $\gamma$. L'équation peut être ramenée à la forme canonique

$$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=1.$$

Les sections de cette surface par les plans passant par l'origine du repère sont toutes des ellipses.

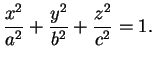
b)Hyperboloïde à une nappe ($H_{1}$) Il s'agit du cas où deux $\alpha_{i}$ sont de même signe, opposé à celui du troisième $\alpha_{i}$ et de $\gamma$. La forme canonique de l'équation est

$$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}-\frac{z^{2}}{c^{2}}=1.$$

On obtient un exemple de cette surface en faisant pivoter une hyperbole autour de son axe imaginaire. Cela engendre une sorte de ``diabolo". C'est parce qu'il est d'un seul tenant(^7.6) qu'on dit que cet hyperboloïde n'a qu'une nappe.

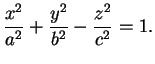
c)Hyperboloïde à deux nappes ($H_{2}$) Il s'agit du cas où deux $\alpha_{i}$ et $\gamma$ sont de même signe, opposé à celui du troisième $\alpha_{i}$. La forme canonique de l'équation est

$$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}-\frac{z^{2}}{c^{2}}=1.$$

Cette fois, il suffit de faire pivoter une hyperbole autour de son axe réel. Chaque branche engendre une partie d'un seul tenant de l'hyperboloïde, donnant ainsi deux nappes.

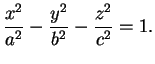
d)Paraboloïde elliptique ($PE$) Il s'agit du cas où deux $\alpha_{i}$ sont de même signe, le troisième $\alpha_{i}$ est nul et $\beta$ ne l'est pas. La forme canonique de l'équation est

$$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=2pz.$$

On obtient un exemple de $PE$ en faisant pivoter une parabole autour de son axe de symétrie.

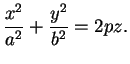
e)Paraboloïde hyperbolique ($PH$) Il s'agit du cas où deux $\alpha_{i}$ sont de signes opposés, le troisième $\alpha_{i}$ est nul et $\beta$ ne l'est pas. La forme canonique de l'équation est

$$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=2pz.$$

Les sections de cette surface par des plans contenant l'axe $O+{\rm I\!R}{\bf e}_{3}$ sont des paraboles. En la coupant par des plans perpendiculaires à cet axe, on obtient des hyperboles. L'une d'elles dégénère en deux droites sécantes en l'origine $O$ du repère. (^7.7)

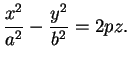
Les propriétés de symétries des quadriques sont très clairement mises en évidence par les équations canoniques. Nous ne les détaillerons pas.

Figure 16: E, $\frac {x^{2}}{a^{2}}+\frac {y^{2}}{b^{2}}+\frac {z^{2}}{c^{2}}=1$ .

Figure 17: H1, $\frac {x^{2}}{a^{2}}+\frac {y^{2}}{b^{2}}-\frac {z^{2}}{c^{2}}=1$.

Figure 18: H1, d'un autre point de vue.

Figure 19: H2, $\frac {x^{2}}{a^{2}}-\frac {y^{2}}{b^{2}}-\frac {z^{2}}{c^{2}}=1$.

Figure 20: PE, $\frac {x^{2}}{a^{2}}+\frac {y^{2}}{b^{2}}=2pz$.

Figure 21: PH, $\frac {x^{2}}{a^{2}}-\frac {y^{2}}{b^{2}}=2pz$.