



suivant: 2.7 Equations paramétriques et
monter: 2.6 Repères et coordonnées
précédent: 2.6 Repères et coordonnées
Table des matières
Un repère de
 est un couple
est un couple
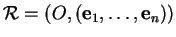 formé d'un point
formé d'un point 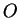 , appelé origine du repère, et d'une base
, appelé origine du repère, et d'une base
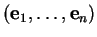 de
de
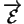 . Les coordonnées (cartésiennes) de
. Les coordonnées (cartésiennes) de
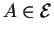 dans ou selon le repère
dans ou selon le repère
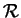 sont les composantes de
sont les composantes de
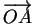 dans la base
dans la base
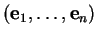 .
.
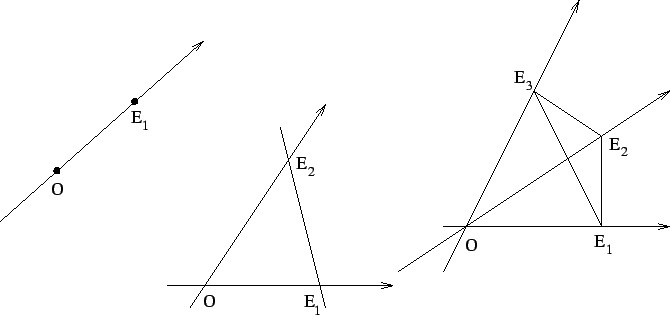
Figure:
Repères, axes et simplexes en dimensions 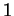 ,
, 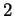 et
et 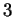 .
.
|
|
Proposition 2.6.1
Si
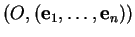
est un repère, alors aucun des points
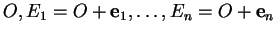
n'est combinaison affine des autres.
Réciproquement, si
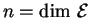
et si aucun des points
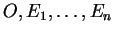
de

n'est combinaison affine des autres, alors
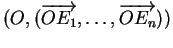
est un repère de

.
Preuve. En effet, le fait qu'aucun des points
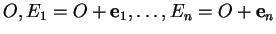 n'est combinaison affine des autres équivaut au fait qu'aucun des
vecteurs
n'est combinaison affine des autres équivaut au fait qu'aucun des
vecteurs
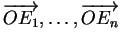 n'est combinaison linéaire
des autres, ce qui signifie qu'ils sont linéairement indépendants.
n'est combinaison linéaire
des autres, ce qui signifie qu'ils sont linéairement indépendants. 
On dit que 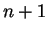 points, où
points, où
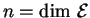 , dont aucun n'est combinaison affine des autres, qu'ils forment un simplexe de
, dont aucun n'est combinaison affine des autres, qu'ils forment un simplexe de
 .
Pour
.
Pour 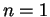 , c'est un segment, pour
, c'est un segment, pour 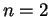 , c'est un triangle et pour
, c'est un triangle et pour 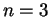 , un tétraèdre. La proposition ci-dessus montre que se donner un repère
, un tétraèdre. La proposition ci-dessus montre que se donner un repère
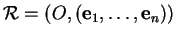 revient à se donner un simplexe
revient à se donner un simplexe
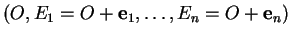 . Le premier point du simplexe est l'origine
du repère. Les autres déterminent les axes
. Le premier point du simplexe est l'origine
du repère. Les autres déterminent les axes 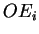 du repère. Ceux-ci sont orientés dans le sens de
du repère. Ceux-ci sont orientés dans le sens de  ,
c'est-à-dire de
,
c'est-à-dire de  vers
vers 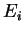 .
.
Si
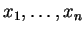 sont les coordonnées de
sont les coordonnées de
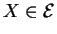 dans le repère
dans le repère
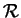 alors on a
alors on a
Le point
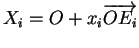 est donc le point de percée de l'axe
est donc le point de percée de l'axe 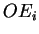 dans l'hyperplan passant par X et parallèle aux autres axes.
De plus,
dans l'hyperplan passant par X et parallèle aux autres axes.
De plus, 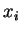 est la mesure algébrique de de
est la mesure algébrique de de
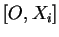 lorsqu'on prend
lorsqu'on prend
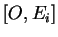 comme étalon de l'axe
comme étalon de l'axe 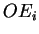 .
.
Figure:
Axes et projections parallèles.
|
|
Remarque 2.6.2
Il est commode d'appeler
la coordonnée de

le point
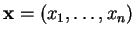
de
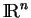
formé des coordonnées de

.
La proposition suivante donne un moyen pratique de calculer la coordonnée de certains points.
Proposition 2.6.3
Dans un repère quelconque, la coordonnée d'une combinaison affine
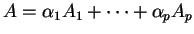
est la combinaison
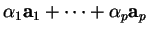
des coordonnées
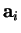
des
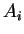
. De même, si
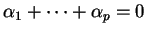
, alors le vecteur des composantes de
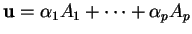
dans la base du repère est
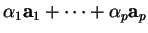
.
Preuve. Cela résulte de ce que
 (
(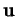 quand
quand
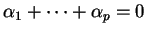 ) vaut
En particulier, les composantes de
) vaut
En particulier, les composantes de
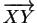 dans la base d'un repère sont celles de
dans la base d'un repère sont celles de
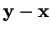 , où
, où 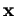 et
et 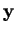 sont les coordonnées de
sont les coordonnées de  et
et 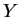 .
.




suivant: 2.7 Equations paramétriques et
monter: 2.6 Repères et coordonnées
précédent: 2.6 Repères et coordonnées
Table des matières
2002-12-17
![]() points, où
points, où
![]() , dont aucun n'est combinaison affine des autres, qu'ils forment un simplexe de
, dont aucun n'est combinaison affine des autres, qu'ils forment un simplexe de
![]() .
Pour
.
Pour ![]() , c'est un segment, pour
, c'est un segment, pour ![]() , c'est un triangle et pour
, c'est un triangle et pour ![]() , un tétraèdre. La proposition ci-dessus montre que se donner un repère
, un tétraèdre. La proposition ci-dessus montre que se donner un repère
![]() revient à se donner un simplexe
revient à se donner un simplexe
![]() . Le premier point du simplexe est l'origine
du repère. Les autres déterminent les axes
. Le premier point du simplexe est l'origine
du repère. Les autres déterminent les axes ![]() du repère. Ceux-ci sont orientés dans le sens de
du repère. Ceux-ci sont orientés dans le sens de ![]() ,
c'est-à-dire de
,
c'est-à-dire de ![]() vers
vers ![]() .
.
![]() sont les coordonnées de
sont les coordonnées de
![]() dans le repère
dans le repère
![]() alors on a
alors on a