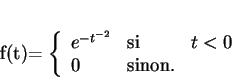suivant: 6.3.2.2 Calculs de la
monter: 6.3.2 Le trièdre de
précédent: 6.3.2 Le trièdre de
Table des matières
A présent, nous choisissons une orientation de  et nous le paramétrons par l'abscisse curviligne
et nous le paramétrons par l'abscisse curviligne  mesurée à partir d'un point
mesurée à partir d'un point  .
Il est commode de désigner les dérivées par rapport à
.
Il est commode de désigner les dérivées par rapport à  par un point:
par un point:
Le vecteur tangent
est normé car le paramétrage
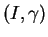 est naturel. Il résulte de la Proposition 2.7 que la dérivée de
est naturel. Il résulte de la Proposition 2.7 que la dérivée de 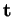 lui est orthogonale.
Intuitivement, elle indique donc la manière dont
lui est orthogonale.
Intuitivement, elle indique donc la manière dont  s'incurve en s'écartant de sa tangente. Sa norme
est la courbure
de
s'incurve en s'écartant de sa tangente. Sa norme
est la courbure
de  en
en
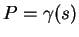 . Si elle n'est pas nulle, on peut écrire
où le vecteur normé
. Si elle n'est pas nulle, on peut écrire
où le vecteur normé
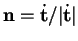 est la normale principale de
est la normale principale de  en
en  .
.
Exemple 6.3.6
Courbure d'une droite
Si 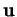 est normé, alors
est normé, alors
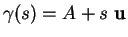 est un paramétrage naturel de la droite
est un paramétrage naturel de la droite
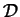 passant par
passant par 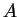 et parallèle à
et parallèle à 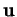 car
car
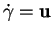 . Comme
. Comme 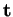 est constant, la courbure de
est constant, la courbure de
 est nulle, conformément à l'intuition.
est nulle, conformément à l'intuition.
Exemple 6.3.7
Courbure d'un cercle
Dans un repère orthonormé, considérons le cercle centré à l'origine et de rayon 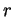 , paramétré comme en (23) par l'abscisse curviligne
, paramétré comme en (23) par l'abscisse curviligne 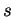 mesurée
depuis
mesurée
depuis 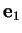 dans le sens trigonométrique.
On a
Par conséquent,
Le fait que la courbure soit l'inverse du rayon est conforme à l'intuition: un cercle tangent à une droite en
dans le sens trigonométrique.
On a
Par conséquent,
Le fait que la courbure soit l'inverse du rayon est conforme à l'intuition: un cercle tangent à une droite en 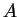 dont le centre s'éloigne le long de la
perpendiculaire en
dont le centre s'éloigne le long de la
perpendiculaire en 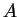 à cette droite, se ``rapproche" de celle-ci à mesure que son rayon croît, c'est-à-dire que
à cette droite, se ``rapproche" de celle-ci à mesure que son rayon croît, c'est-à-dire que 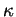 diminue.
diminue.
Figure 6:
Rayon de courbure et courbure.
|
|
En raison de cet exemple,
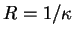 s'appelle le rayon de courbure de
s'appelle le rayon de courbure de  en
en  . On voit de plus que le cercle du plan
. On voit de plus que le cercle du plan
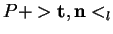 , de centre
, de centre
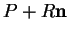 et de rayon
et de rayon 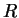 a même tangente, même normale et même courbure
que
a même tangente, même normale et même courbure
que  en
en  . On l'appelle le cercle osculateur de
. On l'appelle le cercle osculateur de  en
en  . Son centre
est le centre de courbure et son plan, le plan osculateur de
. Son centre
est le centre de courbure et son plan, le plan osculateur de  en
en  .
.
Figure:
La concavité est orientée dans le sens de la normale principale.
|
|
Remarque 6.3.8
Quand
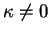
, le développement de Taylor
de
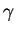
montre que
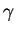
se comporte au voisinage de
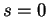
comme la parabole du plan osculateur dont l'équation dans le repère
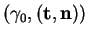
est
Comme
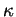
est positif on dit donc que
la concavité de  est orientée dans le sens de la normale principale.
est orientée dans le sens de la normale principale.
Le vecteur
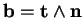 est orthogonal au plan osculateur et est normé. C'est la binormale à
est orthogonal au plan osculateur et est normé. C'est la binormale à  en
en  . Il forme avec
. Il forme avec 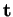 et
et 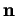 une base
orthonormée positive de
une base
orthonormée positive de
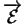 : le trièdre de Frenet
: le trièdre de Frenet
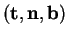 . Il varie bien entendu avec
. Il varie bien entendu avec 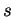 . Voici de quelle façon.
. Voici de quelle façon.
Figure:
Le trièdre de Frenet.
|
|
Proposition 6.3.9
(Formules de Frenet) Lorsque
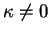
, les dérivées de
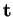
,
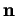
et
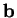
sont données par
où
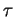
est une fonction de
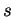
.
Preuve. Puisque 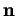 est normé,
est normé,
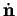 lui est orthogonal (Proposition 2.7). C'est donc une combinaison linéaire de
lui est orthogonal (Proposition 2.7). C'est donc une combinaison linéaire de 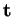 et
et 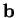 .
On appelle
.
On appelle 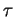 son coefficient selon
son coefficient selon 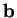 . Pour son coefficient
. Pour son coefficient
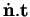 selon
selon 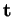 , on a
puisque
, on a
puisque 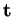 et
et 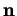 sont orthogonaux et normés. Cela étant,
sont orthogonaux et normés. Cela étant,
D'où le résultat.
Remarque 6.3.10
On peut donner une forme unique aux formules de Frenet. En posant
on voit que
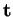
,
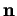
et
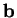
vérifient chacun la relation
La troisième formule de Frenet indique la manière dont la direction du
plan osculateur varie: sa normale 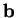 à tendance à ``pivoter" autour de la direction de
la tangente à
à tendance à ``pivoter" autour de la direction de
la tangente à  et ce d'autant plus fort que
et ce d'autant plus fort que 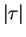 est grand. C'est pourquoi
est grand. C'est pourquoi 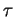 s'appelle la torsion de
s'appelle la torsion de  . Quand elle n'est pas nulle,
. Quand elle n'est pas nulle,
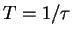 est le rayon de torsion.
est le rayon de torsion.
Preuve. (i) Si  est contenu dans un plan, alors celui-ci se confond avec le plan osculateur de
est contenu dans un plan, alors celui-ci se confond avec le plan osculateur de  . Par conséquent,
. Par conséquent,
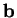 est constant dans
est constant dans 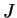 . D'après la troisième formule de Frenet, on en déduit que
. D'après la troisième formule de Frenet, on en déduit que 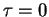 .
.
(ii) Si 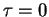 dans
dans 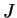 , alors
, alors 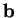 y est constant. On a alors, dans
y est constant. On a alors, dans 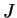 ,
,
où 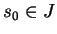 est fixé.
Par conséquent,
ce qui prouve que
est fixé.
Par conséquent,
ce qui prouve que 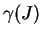 est contenu dans le plan passant par
est contenu dans le plan passant par
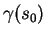 et orthogonal à
et orthogonal à 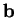 .
.
Quand la courbure s'annule, le plan osculateur peut subir des variations brusques témoignant de discontinuités de la normale principale.
Considérons par exemple le paramétrage de classe 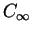
Figure:
Discontinuité de la normale principale quand 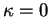 .
.
|
|
où
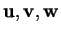 forment une base orthonormée et où les fonctions
forment une base orthonormée et où les fonctions 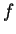 et
et 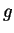 sont données par
sont données par
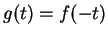 et
Quand
et
Quand 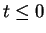 ,
, 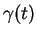 est dans le plan
est dans le plan
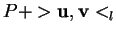 ; quand
; quand 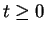 , il est dans le plan
, il est dans le plan
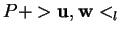 , perpendiculaire au précédent.
En comptant l'abscisse curviligne à partir de
, perpendiculaire au précédent.
En comptant l'abscisse curviligne à partir de  dans l'orientation définie par
dans l'orientation définie par 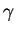 , alors
comme on le voit facilement en appliquant les formules ci-dessous.
, alors
comme on le voit facilement en appliquant les formules ci-dessous.




suivant: 6.3.2.2 Calculs de la
monter: 6.3.2 Le trièdre de
précédent: 6.3.2 Le trièdre de
Table des matières
2002-12-17
![]() et nous le paramétrons par l'abscisse curviligne
et nous le paramétrons par l'abscisse curviligne ![]() mesurée à partir d'un point
mesurée à partir d'un point ![]() .
Il est commode de désigner les dérivées par rapport à
.
Il est commode de désigner les dérivées par rapport à ![]() par un point:
par un point:
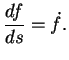
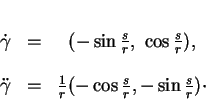
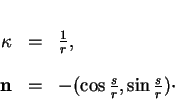
![]() s'appelle le rayon de courbure de
s'appelle le rayon de courbure de ![]() en
en ![]() . On voit de plus que le cercle du plan
. On voit de plus que le cercle du plan
![]() , de centre
, de centre
![]() et de rayon
et de rayon ![]() a même tangente, même normale et même courbure
que
a même tangente, même normale et même courbure
que ![]() en
en ![]() . On l'appelle le cercle osculateur de
. On l'appelle le cercle osculateur de ![]() en
en ![]() . Son centre
est le centre de courbure et son plan, le plan osculateur de
. Son centre
est le centre de courbure et son plan, le plan osculateur de ![]() en
en ![]() .
.
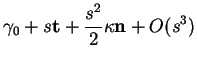
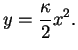
![]() est orthogonal au plan osculateur et est normé. C'est la binormale à
est orthogonal au plan osculateur et est normé. C'est la binormale à ![]() en
en ![]() . Il forme avec
. Il forme avec ![]() et
et ![]() une base
orthonormée positive de
une base
orthonormée positive de
![]() : le trièdre de Frenet
: le trièdre de Frenet
![]() . Il varie bien entendu avec
. Il varie bien entendu avec ![]() . Voici de quelle façon.
. Voici de quelle façon.
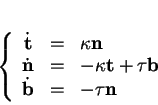
![]() à tendance à ``pivoter" autour de la direction de
la tangente à
à tendance à ``pivoter" autour de la direction de
la tangente à ![]() et ce d'autant plus fort que
et ce d'autant plus fort que ![]() est grand. C'est pourquoi
est grand. C'est pourquoi ![]() s'appelle la torsion de
s'appelle la torsion de ![]() . Quand elle n'est pas nulle,
. Quand elle n'est pas nulle,
![]() est le rayon de torsion.
est le rayon de torsion.
![]() est contenu dans un plan, alors
est contenu dans un plan, alors ![]() dans
dans ![]() .
.
![]() dans
dans ![]() , alors le plan osculateur de
, alors le plan osculateur de ![]() est constant dans
est constant dans ![]() .
.![]() dans
dans ![]() , alors
, alors ![]() y est constant. On a alors, dans
y est constant. On a alors, dans ![]() ,
,
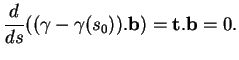
![]()