5.2.1 Définition

Une application ${\mathcal T}$ d'un espace affine ${\mathcal E}$ dans lui-même est affine si elle préserve les combinaisons affines, c'est-à-dire si

$${\mathcal T}(\alpha_1A_1+ \cdots + \alpha_pA_p)=\alpha_1 {\mathcal T}(A_1)+ \cdots +\alpha_p {\mathcal T}(A_p)$$

pour tous $A_1, \cdots ,A_p \in {\mathcal E}$ et tous $\alpha_1, \cdots ,\alpha_p \in {\rm I\!R}$ dont la somme vaut $1$. En particulier, une application affine transforme des points alignés en des points alignés. (^5.1)

Exemple 5.2.1   Les translations

Chaque translation de ${\mathcal E}$ est une application affine. En effet, $S\in {\mathcal E}$ étant arbitrairement choisi,

$$\alpha_1t_{{\bf u}}(A_1)+ \cdots + \alpha_pt_{{\bf u}}(A_p)-S = \alpha_1\overrightarrow{S(t_{\bf u}(A_1))}+ \cdots + \alpha_p\overrightarrow{S(t_{\bf u}(A_p))}$$

$$= \alpha_1(\overrightarrow{SA_1}+{\bf u})+ \cdots + \alpha_p(\overrightarrow{SA_p}+{\bf u})$$

$$= \alpha_1\overrightarrow{SA_1}+ \cdots + \alpha_p\overrightarrow{SA_p}+{\bf u}$$

$$= t_{{\bf u}}(\alpha_1A_1+ \cdots + \alpha_pA_p) -S$$

pour autant que la somme des $\alpha_i$ soit $1$.

Exemple 5.2.2   Les homothéties

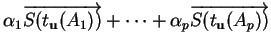Par définition, l'homothétie de centre $C\in {\mathcal E}$ et de rapport $k \in {\rm I\!R}$ est l'application ${\mathcal H}_{C, k}$ définie par

$$X \mapsto C+k\overrightarrow{CX}.$$

Figure: $P'Q'R'$ est l'image de $PQR$ par l'homothétie de centre $C$ et de rapport $-1/2$.

Elle transforme donc un point $X (\ne C)$ en un point $Y$ de la droite $CX$ dont la mesure algébrique par rapport à l'étalon $\lbrack C,X \rbrack$ est $k$: $\overrightarrow{CY}=k\overrightarrow{CX}$. Le point $C$ est transformé en lui-même. On dit que c'est un point fixe de ${\mathcal H}_{C, k}$. L'homothétie ${\mathcal H}_{C, k}$ est une application affine. En effet,

$$\alpha_1{\mathcal H}_{C, k}(A_1)+ \cdots + \alpha_p{\mathcal H}_{C, k}(A_p)-C = \alpha_1(k\overrightarrow{CA_1})+ \cdots + \alpha_p(k\overrightarrow{CA_p})$$

$$= k(\alpha_1\overrightarrow{CA_1}+ \cdots + \alpha_p\overrightarrow{CA_p})$$

$$= k(\alpha_1 A_1+ \cdots + \alpha_p A_p-C)$$

$$= {\mathcal H}_{C, k}(\alpha_1 A_1+ \cdots + \alpha_p A_p)-C.$$

L'homothétie ${\mathcal H}_{C,-1}$ est la symétrie centrale $s_C$ par rapport à $C$, dans laquelle un point et son image forment toujours un segment dont $C$ est le milieu.

Figure: Symétrie centrale

Proposition 5.2.3   Pour $k\ne0$, l' homothétie ${\mathcal H}_{C, k}$ transforme chaque droite ne passant pas par $C$ en une droite parallèle et chaque droite passant par $C$ en elle-même.

Preuve. C'est immédiat: ${\mathcal H}_{C, k}$ transforme une droite $AB$ en une droite admettant le vecteur-directeur $k\overrightarrow{AB}$.$\qed$

En application de la propriété ci-dessus, on vérifie que la droite qui joint les milieux $B'$ et $C'$ des côtés $[A, B]$ et $[A, C]$ d'un triangle $ABC$ est parallèle à $BC$. En effet, $B'C'$ est l'image de $BC$ par l'homothétie de centre $A$ et de rapport $1/2$.

Figure: $B'C'$ est l'image de $BC$ par l'homothétie ${\mathcal H}_{A, 1/2}$.

Voici une autre application de la même propriété. Le fait que les médianes de $ABC$ se coupent en le centre de gravité G, au deux tiers de chacune depuis le sommet dont elle est issue, se traduit par le fait que l'homothétie de centre G et de rapport -1/2 transforme chaque sommet en le milieu du côté opposé. Elle transforme donc les hauteurs du triangle en ses médiatrices. Celles-ci se coupent évidemment en le centre de la circonférence circonscrite au triangle. Par conséquent, ses hauteurs sont également concourantes et, de plus, leur point d'intersection (l'orthocentre du triangle), le centre du cercle circonscrit et le centre de gravité sont alignés.

La proposition suivante résulte immédiatement de la définition des applications affines.

Proposition 5.2.4   La composée d'applications affines est une application affine. L'inverse d'une bijection affine est une application affine.

Comme l'identité $id_{\mathcal E}$ de ${\mathcal E}$ dans lui-même est une application affine, on voit que l'ensemble des bijections affines de ${\mathcal E}$, qu'on appelle les affinités de ${\mathcal E}$, est un groupe pour la composition des applications, le groupe affine de ${\mathcal E}$.