



suivant: 4.4.2.4 Projection orthogonale d'un
monter: 4.4.2 Distance entre variétés
précédent: 4.4.2.2 Distance d'un point
Table des matières
Nous allons exprimer la distance entre deux droites
 et
et
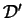 d'équations vectorielles
d'équations vectorielles
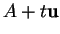 et
et
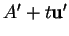 lorsque
lorsque
 est de dimension trois et orienté.
Nous supposons que les droites sont gauches. En particulier,
est de dimension trois et orienté.
Nous supposons que les droites sont gauches. En particulier, 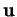 et
et 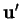 sont linéairement indépendants.
sont linéairement indépendants.
La distance entre
 et
et
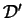 est la même que celle de
est la même que celle de 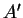 au plan
au plan  contenant
contenant
 et parallèle
à
et parallèle
à
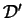 de sorte que
de sorte que
puisque
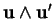 est une normale à
est une normale à  .
En effet, d'une part la distance entre
.
En effet, d'une part la distance entre
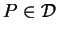 et
et
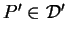 est aussi la distance entre
est aussi la distance entre
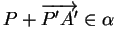 et
et 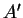 (car la distance est invariante par translation). Donc
Ce qui implique
(car la distance est invariante par translation). Donc
Ce qui implique
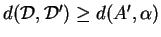 .
.
D'autre part, la parallèle à
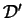 menée par la projection orthogonale
menée par la projection orthogonale 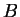 de
de 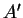 sur
sur  coupe
coupe
 en un point
en un point 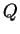 et la distance entre
et la distance entre 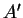 et
et 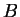 est la même que celle séparant
est la même que celle séparant 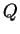 et
et
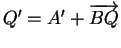 . Donc
. Donc
D'où l'affirmation.
Figure 6:
Distance de deux droites gauches...
|
|
Il ressort de ce qui précède que
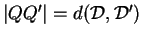 et que
et que 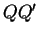 est perpendiculaire à
est perpendiculaire à
 et à
et à
 . C'est la perpendiculaire commune aux deux
droites (4.4).
. C'est la perpendiculaire commune aux deux
droites (4.4).




suivant: 4.4.2.4 Projection orthogonale d'un
monter: 4.4.2 Distance entre variétés
précédent: 4.4.2.2 Distance d'un point
Table des matières
2002-12-17
![]() et
et
![]() est la même que celle de
est la même que celle de ![]() au plan
au plan ![]() contenant
contenant
![]() et parallèle
à
et parallèle
à
![]() de sorte que
de sorte que
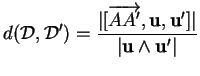
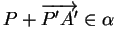 et
et ![]() menée par la projection orthogonale
menée par la projection orthogonale ![]() de
de ![]() sur
sur ![]() coupe
coupe
![]() en un point
en un point ![]() et la distance entre
et la distance entre ![]() et
et ![]() est la même que celle séparant
est la même que celle séparant ![]() et
et
![]() . Donc
. Donc
![]() et que
et que ![]() est perpendiculaire à
est perpendiculaire à
![]() et à
et à
![]() . C'est la perpendiculaire commune aux deux
droites (4.4).
. C'est la perpendiculaire commune aux deux
droites (4.4).