- ... ouvertes(1.1
- Pour ne pas alourdir les notations, on ne mentionne pas explicitement la dimension
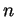 dans l'écriture ci-dessous. Le contexte devrait normalement lever l'ambiguïté qui pourrait résulter de cette convention.
dans l'écriture ci-dessous. Le contexte devrait normalement lever l'ambiguïté qui pourrait résulter de cette convention.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(1.2
- Cette propriété sert souvent définition des fermés de
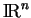 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(1.3
- On rappelle que pour tout ensemble
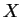 ,
, 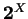 désigne l'ensemble des parties de
désigne l'ensemble des parties de 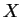 :
:
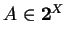 équivaut donc à
équivaut donc à
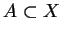 . Ainsi, si
. Ainsi, si
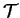 est une topologie sur
est une topologie sur 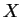 , alors on peut écrire
, alors on peut écrire
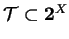
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... réels(1.4
- C'est une notation classique.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(1.5
- On les appelle les fonctions invariantes élémentaires car tout polynôme (et même toute fonction de classe
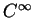 ) invariant défini sur
) invariant défini sur
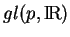 est un polynôme (une fonction de même classe, respectivement) en ces fonctions
est un polynôme (une fonction de même classe, respectivement) en ces fonctions
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(2.1
- Le nombre
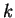 n'est pas précisé. C'est un entier positif. Il détermine la classe du paramétrage. Pratiquement, nous n'aurons affaire qu'à des paramétrage de classe
n'est pas précisé. C'est un entier positif. Il détermine la classe du paramétrage. Pratiquement, nous n'aurons affaire qu'à des paramétrage de classe 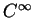 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (2.2
- Ceci assure que le rang de
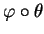 soit le bon mais aussi que
soit le bon mais aussi que
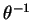 , et donc
, et donc
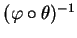 , soit continu.
, soit continu.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... intervalles(2.3
- Ceci n'est pas tout à fait immédiat.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(2.4
- La notation
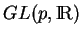 désigne le sous-ensemble de
désigne le sous-ensemble de
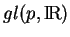 formé des matrices non singulières. Cet ensemble est un ouvert de
formé des matrices non singulières. Cet ensemble est un ouvert de
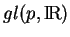 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... quadriques(3.1
- Par exemple, nous nous limiterons à une classification affine.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(3.2
- C'est un changement de coordonnées supplémentaire...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... matricielle(3.3
- C'est même un groupe de Lie dans la mesure où cette multiplication et le passage à l'inverse sont des applications de classe
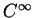 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... notes(3.4
- Il s'agit d'une version faible du résultat de E. Cartan. Le théorème général affirme que tout sous-groupe fermé d'un groupe de Lie à base dénombrable en est un sous-groupe de Lie plongé.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (3.5
- Pour rappel, l'effet d'un changement de variables sur une intégrale consiste à multiplier l'intégrand par la valeur absolue du Jacobien du changement de variables.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(3.6
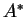 désigne la matrice conjuguée et
transposée de
désigne la matrice conjuguée et
transposée de 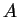
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(4.1
- L'espace projectif réel de dimension
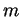 est l'ensemble
est l'ensemble
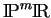 des droites vectorielles de
des droites vectorielles de
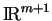 . C'est une variété au sens de
la géométrie différentielle abstraite mais il n'est pas facile, en
général, de le réaliser comme variété plongée dans un espace
euclidien.
. C'est une variété au sens de
la géométrie différentielle abstraite mais il n'est pas facile, en
général, de le réaliser comme variété plongée dans un espace
euclidien.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(5.1
- On dit alors que
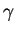 est une courbe de ou tracée sur
est une courbe de ou tracée sur  et passant par
et passant par  en
en 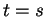 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
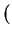 5.2
5.2
- Remarquons que cette équation est
identiquement nulle lorsque $a$ est un point double de $Q$.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(5.3
- X est de classe
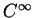 en
en 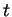 et
et
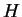 et dépend de ceux-ci par l'intermédiaire de leur produit.
et dépend de ceux-ci par l'intermédiaire de leur produit.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(5.4
- Bien noter
que cette propriété ne s'étend pas à des "exposants" non proportionnels: en général,
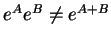 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(5.5
- Nous supposons
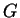 de classe
de classe
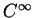 . C'est le cas des exemples donnés plus haut mais on peut montrer que c'est en fait toujours le cas.
. C'est le cas des exemples donnés plus haut mais on peut montrer que c'est en fait toujours le cas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(5.6
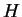 étant un vecteur tangent à
étant un vecteur tangent à 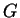 en
en 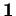 , il est dans l'image de
, il est dans l'image de
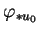 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
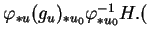 5.7
5.7
- On
aimerait écrire que cette dernière expression est égale à
$(&phiv#varphi;&cir#circ;g_u&cir#circ;&phiv#varphi;^-1)_*u_0H$. C'est exact mais nous
n'en n'avons pas les
moyens. En effet, il faudrait pour cela savoir prendre l'application
linéaire tangente de $&phiv#varphi;^-1$ qui n'est cependant pas défini
dans un ouvert de
$ I&negsp;R^m$. En fait $&phiv#varphi;^-1$ est un exemple d'application
différentiable entre variétés plongées, notion que nous n'aborderons
pas ici.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... par(5.8
- Ceci se voit sans difficulté
en calculant explicitement le produit
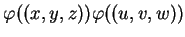 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
forme(5.9
- Lorsque la dimension de
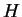 est
est 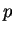 , l'exponentielle
de
, l'exponentielle
de 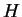 peut toujours être exprimée comme combinaison linéaires des
puissances
peut toujours être exprimée comme combinaison linéaires des
puissances
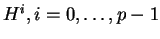 , de
, de 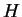 . Cela résulte du fait que
. Cela résulte du fait que 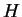 annule son
polynôme caractéristisque
annule son
polynôme caractéristisque
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
(5.10
- Dans un produit cartésien, le crochet de Lie est défini
composante à composante.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (5.11
- La
matrice
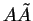 est non singulière car
est non singulière car 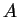 est de rang
est de rang 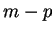 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (5.12
- Cela signifie
que
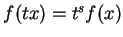 pour tout
pour tout
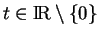 et tout
et tout 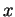 appartenant au domaine
de
appartenant au domaine
de  , que nous supposerons être
, que nous supposerons être
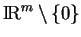 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (5.13
- Cette inégalité
classique
est plus simple à démontrer grâce aux fonctions convexes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... droite(5.14
- En admettant que dans un espace
euclidien la droite
minimise la distance entre deux points quelconques, ce que nous
n'avons pas établi ici.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(5.15
- Nous ne donnerons pas la démonstration de ce fait, qui relève de
l'analyse.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(5.16
- comprendre: pour
toute valeur de
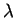
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(5.17
- Elle n'est définie que dans
l'ensemble des
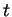 en lesquels
en lesquels
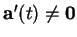 . Ce n'est pas nécessairement un arc régulier de courbe.
. Ce n'est pas nécessairement un arc régulier de courbe.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(6.1
- Les dérivées
sont calculées en le point
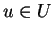 tel que
tel que
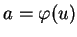 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... angles(6.2
- Le lecteur est invité à le vérifier.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (6.3
- C'est
ici une écriture symbolique; elle
s'interprète de façon tout à fait rigoureuse en termes de tenseurs symétriques covariants, notions que nous n'étudions pas
dans ce texte.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(6.4
- L'unicité n'est garantie que pour les géodésiques
maximales, c'est-à-dire
définies sur un intervalle
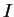 maximal.
maximal.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... métrique(6.5
- La topologie d'espace métrique d'un ensemble muni d'une distance
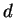 est celle dont les ouverts sont les unions de boules ouvertes de
est celle dont les ouverts sont les unions de boules ouvertes de 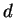 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... demandée(6.6
- Pour rappel, si
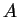 est un intervalle ouvert de
est un intervalle ouvert de
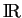 de longueur au plus
de longueur au plus 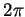 , alors
est un homéomorphisme de
, alors
est un homéomorphisme de 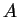 sur son image.
sur son image.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... donc(6.7
- Pour la notion de mesure dans un espace vectoriel ou affine, voir l'annexe.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(6.8
- Le volume de celui-ci est
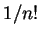 fois celui du
parallélépipède construit sur les mêmes vecteurs.
fois celui du
parallélépipède construit sur les mêmes vecteurs.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(6.9
- C'est donc la
valeur absolue de leur produit mixte défini dans cet hyperplan par
une quelconque de ses
orientations.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(6.10
- L'annexe en fin de texte présente d'autres arguments. On y explique entre autre les liens entre la notion d'élément de surface et de densité.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... cylindre(6.11
- En effet, la longueur d'un arc de cercle de rayon
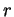 vu sous un angle
vu sous un angle 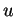 depuis le centre est
depuis le centre est 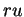 , pour autant que
l'angle soit mesuré en radians.
, pour autant que
l'angle soit mesuré en radians.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (6.12
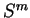 est la sphère de centre 0 et de
rayon
est la sphère de centre 0 et de
rayon 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(6.13
- La normale principale
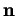 et la courbure
et la courbure 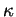 d'un arc régulier de courbe de
d'un arc régulier de courbe de
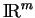 sont définis comme dans le cas des courbes de
sont définis comme dans le cas des courbes de
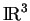 par la formule
par la formule
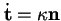 ,
, 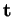 étant la normale unitaire définie par un paramétrage de l'arc par une abscisse curviligne.
étant la normale unitaire définie par un paramétrage de l'arc par une abscisse curviligne.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
(6.14
- Pour les surfaces plongées dans
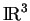 , c'est un théorème dû à Gauss.
, c'est un théorème dû à Gauss.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (7.1
- Ouverte ou fermée, cela ne change essentiellement rien dans ce qui va suivre.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(7.2
- En fait, on peut montrer que c'est un polynôme de degré
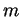 dans
dans
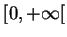
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (7.3
- Par exemple si l'intéreur de
 n'est pas vide.
n'est pas vide.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (7.4
- Si
 est inclus dans
est inclus dans 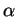 , n'importe quelle normale à celui-ci fait l'affaire. Du reste, il est alors évident que
, n'importe quelle normale à celui-ci fait l'affaire. Du reste, il est alors évident que 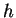 est parallèle à
est parallèle à 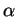 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (7.5
- Un homéomorphisme est une bijection continue dont la réciproque est continue. En topologie, on ne distingue pas deux espaces qui sont homéomorphes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (7.6
- Ce qui suffit: si
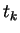 ne converge pas vers
ne converge pas vers 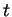 , il admet une sous-suite dont les éléments sont à une distance de
, il admet une sous-suite dont les éléments sont à une distance de 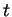 qui n'est pas inférieur à un certain
qui n'est pas inférieur à un certain
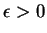 . On ne saurait extraire de celle-ci une sous-suite convergeant vers
. On ne saurait extraire de celle-ci une sous-suite convergeant vers 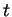 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(7.7
- Dans l'enseignement secondaire, on dit de
 qu'il tourne sa concavité ``vers le haut''.
qu'il tourne sa concavité ``vers le haut''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(7.8
- La combinaison
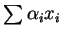 est alors dite convexe.
est alors dite convexe.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... que(7.9
- Les dérivées partielles sont calculées en
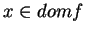
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... pointe(7.10
- Cela veut dire que
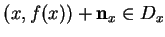 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(7.11
- Appliquer de nouveau le théorème de Lebesgue après avoir constaté que les fonctions caractéristiques des ensembles considérés convergent vers celles de
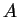 ,
, 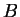 et de leur somme.
et de leur somme.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.