Quitte à le translater, ce qui ne restreint pas la portée de ce qui suit, et choisir ![]() assez petit, nous pouvons supposer que
assez petit, nous pouvons supposer que ![]() contient la boule
contient la boule ![]() de centre 0 et de rayon
de centre 0 et de rayon ![]() . Posons
. Posons
![]() .
.
b) ... et en un seul. En effet, supposons que
![]() , soit un point frontière de
, soit un point frontière de ![]() . Par convexité, tous les segments joignant un point de
. Par convexité, tous les segments joignant un point de ![]() à
à ![]() sont contenus dans
sont contenus dans ![]() . Les points
. Les points ![]() ,
, ![]() , sont donc intérieurs à
, sont donc intérieurs à ![]() . Nous noterons
. Nous noterons
![]() le point frontière de
le point frontière de ![]() de la forme
de la forme ![]() ,
,
![]() .
.
c) Il est clair que
![]() et
et ![]() sont des applications réciproques l'une de l'autre. La première est continue car c'est la restriction d'une application continue de
sont des applications réciproques l'une de l'autre. La première est continue car c'est la restriction d'une application continue de
![]() dans
dans
![]() . Vérifions que
. Vérifions que ![]() l'est aussi. Soit une suite
l'est aussi. Soit une suite
![]() convergeant vers
convergeant vers ![]() . Posons
. Posons
![]() et
et
![]() . Nous allons vérifier que
. Nous allons vérifier que
![]() en montrant que de toute sous-suite de
en montrant que de toute sous-suite de ![]() , on peut extraire une sous-suite qui converge vers
, on peut extraire une sous-suite qui converge vers ![]() (7.6). Pour alléger les notations, nous appellons encore
(7.6). Pour alléger les notations, nous appellons encore ![]() la sous-suite. La suite
la sous-suite. La suite ![]() , bornée, admet une sous-suite convergente dont nous notons
, bornée, admet une sous-suite convergente dont nous notons ![]() la limite. Puisque
la limite. Puisque ![]() est fermé,
est fermé,
![]() . Vu l'unicité prouvée en b), c'est donc
. Vu l'unicité prouvée en b), c'est donc
![]() .
.![]()
Nous notons encore ![]() la réciproque de la restriction de
la réciproque de la restriction de ![]() à la frontière de
à la frontière de ![]() .
.
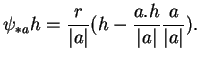
Soit un paramétrage local
![]() de
de ![]() .
En le composant avec
.
En le composant avec ![]() , on obtient un paramétrage local
, on obtient un paramétrage local
![]() de
de ![]() :
:
![]() est injectif, de même que sa différentielle; de plus, vu la proposition précédente, sa réciproque est continue.
est injectif, de même que sa différentielle; de plus, vu la proposition précédente, sa réciproque est continue.
Soient à présent un paramétrage
![]() d'un ouvert
d'un ouvert ![]() de
de ![]() et un point quelconque
et un point quelconque ![]() de
de ![]() . On peut choisir
. On peut choisir
![]() pour que
pour que ![]() soit un voisinage de
soit un voisinage de
![]() contenu dans
contenu dans
![]() .
Les paramétrages
.
Les paramétrages
![]() et
et
![]() de
de ![]() étant localement équivalents, il existe un changement de variables régulier
étant localement équivalents, il existe un changement de variables régulier
![]() tel que
tel que
![]() . On a alors
. On a alors
![]() , ce qui montre que
, ce qui montre que
![]() définit un paramétrage de
définit un paramétrage de ![]() dans
dans ![]() .
.
Pour paramétrer le complémentaire d'un point de ![]() , il suffit donc de paramétrer le complémentaire d'un point d'une sphère. Ceci se fait par exemple grâce aux projections stéréographiques.
, il suffit donc de paramétrer le complémentaire d'un point d'une sphère. Ceci se fait par exemple grâce aux projections stéréographiques.![]()
Pour le reste de ce paragraphe, nous supposons que ![]() est un paramétrage du complémentaire d'un point (noté
est un paramétrage du complémentaire d'un point (noté ![]() dans la suite) de
dans la suite) de ![]() . Nous notons
. Nous notons ![]() la normale orientée vers l'extérieur de
la normale orientée vers l'extérieur de ![]() . Nous pouvos supposer que c'et celle ssociée au paramétrage
. Nous pouvos supposer que c'et celle ssociée au paramétrage ![]() Nous allons à présent vérifier que
Nous allons à présent vérifier que ![]() est un polynôme en
est un polynôme en ![]() pour
pour ![]() assez petit.
assez petit.
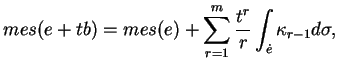
Il est assez évident que
![]() est une bijection: si
est une bijection: si ![]() alors
alors ![]() est la projection de
est la projection de ![]() sur
sur ![]() , ce qui le détermine univoquement, ainsi que
, ce qui le détermine univoquement, ainsi que ![]() .
.
Calculons le déterminant de la différentielle de ![]() . En notant
. En notant
![]() la dérivée par rapport à
la dérivée par rapport à ![]() , il vient
, il vient
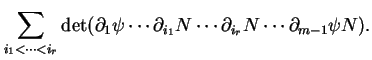
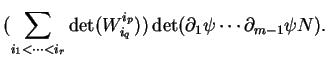
D'après le théorème de la fonction inverse, ![]() est donc un changement de variables régulier entre
est donc un changement de variables régulier entre
![]() et son image. On a donc
et son image. On a donc
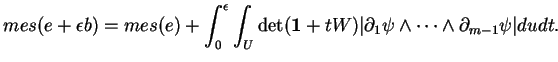
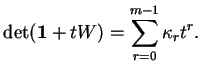
Comme signalé plus haut, cette proposition donne lieu à l'inégalité isopérimétrique pour les convexes compacts d'intérieur non vide dont la frontière est une variété plongée, inégalité qui sera validée dès que nous aurons établi l'inégalité de Brun-Minkowski. Elle est en fait vraie dans l'ensemble de tous les convexes compacts non vides, mais nous ne le démontrerons pas.
Voici un autre corollaire de cette proposition. C'est un cas particulier d'un théorème très général de géométrie différentielle, le théorème de Gauss-Bonnet.
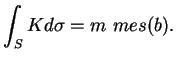
Cette proposition résulte aussi du Corollaire 52. En effet, pour une hypersurface ![]() comme dans l'énoncé, la surface de l'image de
comme dans l'énoncé, la surface de l'image de ![]() sous l'application de Gauss
sous l'application de Gauss ![]() est la sphère tout entière.
est la sphère tout entière.