1.2.2 Exemples

La différentielle de $f:(x,y)\mapsto (x+y,xy,\frac{x}{y}+\frac{y}{x})$ en $a=(u,v), \ u,v\neq 0,$ existe et est représentée par la matrice

$$% latex2html id marker 16405\left ( \begin{array}{ccc} 1&1... ... \frac{u^2-v^2}{u^2v}&\frac{v^2-u^2}{v^2u} \end{array}\right )$$

De fait, si $h=(p,q)$, alors $f(a+th)$ vaut

$$(u+v+t(p+q),uv+t(vp+uq)+t^2pq,\frac{u+tp}{v+tq}+\frac{v+tq}{u+tp})$$

En vertu du théorème de dérivation des fonctions composées, ceci admet une dérivée en $t=0$ qui est donnée par

$$(p+q,vp+uq,\frac{vp-uq}{v^2}+\frac{uq-vp}{u^2})$$

et que l'on obtient bien en appliquant la matrice ci-dessus à $h$.

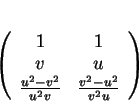
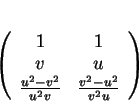
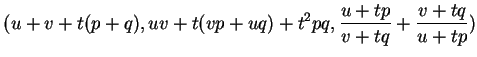
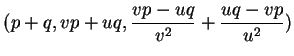
Dans ce texte, on désigne par $gl(p,{\rm I\!R})$ l'espace ${\rm I\!R}^p_p$ des matrices ayant $p$ lignes et $p$ colonnes de nombres réels(^1.4). Il est canoniquement isomorphe à ${\rm I\!R}^{p^2}$ avec lequel nous le confondrons.

Lemme 4   La différentielle de $\det:A\mapsto \det(A)$, fonction de la matrice carrée $A\in gl(p,{\rm I\!R})$, est l'application linéaire

$$H\in gl(p,{\rm I\!R})\mapsto {\rm tr}(\tilde{{\mathcal A}}H)\in{\rm I\!R},$$

où ${\mathcal A}$ désigne la matrice des mineurs (algébriques) de $A$. En particulier, si $A$ est non singulier, alors $\det_{*A}H=\det(A){\rm tr}(A^{-1}H)$.

Le déterminant $\det(A+tH)$ est un polynôme en $t$. Nous devons en trouver le coefficient du terme du premier degré. Développons-le (en pensée) à l'aide des propriétés de $\det$ vis-à-vis des colonnes. Chaque colonne $A_i+tH_i$ de $A+tH$ donne, indépendamment des autres, deux contributions: celle où on la remplace par $A_i$ et celle où on la remplace par $tH_i$. Cette dernière permet de mettre $t$ en facteur des termes où elle apparaît. Pour le terme du premier degré en $t$, il faut donc collecter les termes où une seule colonne de $A+tH$ a été remplacée par la colonne de même numéro de $tH$. On obtient dès lors le coefficient

$$\sum_{i=1}^p\det( \underbrace{A_1\ldots H_i}_{i \mbox{ \tiny colonnes}}\ldots A_p)$$

On l'évalue en appliquant la règle des mineurs à la colonne $i$ pour calculer le terme numéro $i$, ce qui donne

$$\sum_{ij}{\mathcal A}^j_iH^j_i={\rm tr}(\tilde{{\mathcal A}}H).$$

$\qedsymbol$

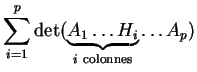
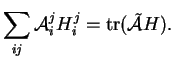
Quand $A$ est non singulier, on peut écrire le développement complet de $\det(A+tH)$.

Remarque 5   Si $\det A\neq 0$, alors

$$\det (A+tH)=\det(A)\sum_{i=0}^pt^i\chi_i(A^{-1}H).$$ (1.2)

Les fonctions $\chi: gl(p,{\rm I\!R})\mapsto {\rm I\!R}$ sont définies par

$$\det(M-\lambda{\bf 1})=\sum_{i=0}^p(-1)^{p-i}\lambda^{p-i}\chi_i(M).$$ (1.3)

Comme pour $S$ non singulier,

$$\det S(M-\lambda{\bf 1})S^{-1}=\det(M-\lambda{\bf 1})$$

on a

$$\chi_i(SMS^{-1})=\chi_i(M).$$

On dit dès lors que les fonctions sont invariantes sous l'action du groupe des matrices non singulières de dimension $p$(^1.5). On a $\chi_0(M)=1$ et, pour $i>0$, $\chi_i(M)$ est la somme des déterminants des matrices carrées de dimension $i$ extraites de $M$ en sélectionnant $i$ lignes et les $i$ colonnes de mêmes numéro. C'est évident lorsque $M$ est diagonal. C'est encore vrai lorsque $M$ est diagonalisable, par invariance. C'est enfin vrai pour $M$ quelconque car les matrices diagonalisables sont denses dans $gl(p,{\rm I\!R})$ et les fonctions $\chi_i$ sont manifestement continues. La fonction $\chi_1$ est donc la somme des éléments diagonaux. C'est la trace. Bien entendu, $\chi_p$ est la fonction $\det$. Il résulte immédiatement de la formule (3) que $\chi_i(M)$ vaut encore la somme des produits de $i$ valeurs propres de $M$.

Cela étant, la formule (2) est une conséquence facile de (3).

Dans (2), le coefficient de degré $1$ en $t$ est

$$\det(A){\rm tr}(A^{-1}H)$$

On obtient immédiatement

$${\det} _{*A} H={\rm tr}(\tilde{{\mathcal A}}H)$$

pour $A$ non singulier. Par continuité, c'est encore vrai pour $A$ singulier.