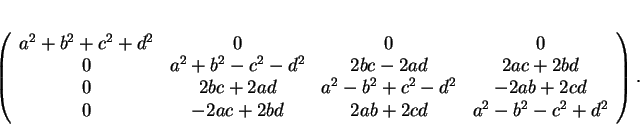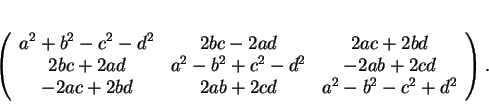Tout quaternion ![]() admet une décomposition polaire
admet une décomposition polaire
![]() ), où
), où ![]() est un quaternion tel que
est un quaternion tel que ![]() .
Si
.
Si ![]() et si
et si
![]() alors cette décomposition est
déterminée par les relations
alors cette décomposition est
déterminée par les relations
![]() et
et
![]() .
L'argument
.
L'argument ![]() de
de ![]() est déterminé à des multiples de
est déterminé à des multiples de
![]() près et l'unité
près et l'unité ![]() est unique, sauf si
est unique, sauf si
![]() ,
c'est-à-dire si
,
c'est-à-dire si ![]() est réel.
Lorsque
est réel.
Lorsque ![]() , la décomposition est indéterminée.
, la décomposition est indéterminée.
Dans ce qui suit, on munit
![]() de la structure d'espace vectoriel euclidien orienté pour laquelle
de la structure d'espace vectoriel euclidien orienté pour laquelle ![]() est une base orthonormée positive. Pour rappel, à l'exception de l'identité, chaque rotation
est une base orthonormée positive. Pour rappel, à l'exception de l'identité, chaque rotation ![]() de
de
![]() possède un axe
possède un axe
![]() . Le fait d'orienter cet axe par un vecteur directeur unitaire
. Le fait d'orienter cet axe par un vecteur directeur unitaire ![]() oriente automatiquement son complément orthogonal: les bases positives de ce dernier complétées par
oriente automatiquement son complément orthogonal: les bases positives de ce dernier complétées par ![]() forment des bases positives de
forment des bases positives de
![]() . L'angle de la rotation
. L'angle de la rotation ![]() est alors celui de la rotation qu'elle induit dans
est alors celui de la rotation qu'elle induit dans
![]() . Comme il y a deux manières d'orienter
. Comme il y a deux manières d'orienter
![]() , il y a également deux possibilités d'associer un angle à
, il y a également deux possibilités d'associer un angle à ![]() . Elles s'interprètent commodément en terme de quaternions.
. Elles s'interprètent commodément en terme de quaternions.
On désigne par ![]() la multiplication à droite
la multiplication à droite
![]() par
par ![]() . Dans la base
. Dans la base ![]() , elle est représentée par la matrice
, elle est représentée par la matrice
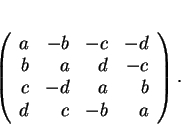
La proposition précédente montre que ![]() est le quotient du
groupe
est le quotient du
groupe ![]() par le sous-groupe
par le sous-groupe ![]() . Chaque droite vectorielle
de
. Chaque droite vectorielle
de
![]() coupe
coupe ![]() en
une classe d'équivalence
en
une classe d'équivalence ![]() définissant ce quotient et,
réciproquement, chaque classe est obtenue de la sorte. On peut donc
identifier
définissant ce quotient et,
réciproquement, chaque classe est obtenue de la sorte. On peut donc
identifier ![]() et
l'ensemble
et
l'ensemble
![]() des droites vectorielles de
des droites vectorielles de
![]() qu'on
appelle l'espace projectif réel de dimension
qu'on
appelle l'espace projectif réel de dimension
![]() (4.1).
(4.1).
En utilisant les matrices représentant ![]() et
et ![]() dans la base
dans la base ![]() , on obtient la matrice représentant
, on obtient la matrice représentant
![]() . Les composantes de
. Les composantes de ![]() étant
étant
![]() , il s'agit de
, il s'agit de