



suivant: 7.3.3 Convexité & hessien
monter: 7.3 Fonctions convexes
précédent: 7.3.1 Inégalité de Jensen
Table des matières
Lorsque le domaine de  est un ouvert dans lequel
est un ouvert dans lequel  est de classe
est de classe 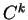 ,
, 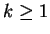 , son graphe
, son graphe
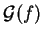 est une hypersurface, dont
est une hypersurface, dont
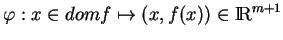 est un paramétrage. Il est facile de voir que(7.9)
Nous notons
est un paramétrage. Il est facile de voir que(7.9)
Nous notons 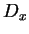 l'intersection de
l'intersection de
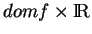 et du demi-espace délimité par l'espace tangent en
et du demi-espace délimité par l'espace tangent en
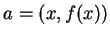 à
à
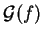 et vers lequel
et vers lequel 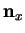 pointe(7.10). Un point
pointe(7.10). Un point
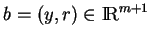 appartient à
appartient à 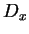 si et seulement si
si et seulement si
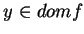 et
et
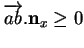 .
.
Lemme 67
Si
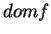
est un ouvert convexe dans lequel

est de classe
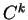
,
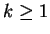
, alors
De plus,

est convexe si et seulement si
Soit un point 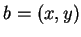 de l'intersection des
de l'intersection des 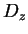 . On a
. On a
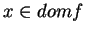 . Posons
. Posons
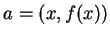 . Le fait que
. Le fait que 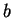 soit dans
soit dans 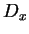 se traduit alors par
c'est-à-dire
se traduit alors par
c'est-à-dire
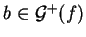 .
.
Si
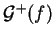 est égal à l'intersection des
est égal à l'intersection des 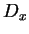 , alors il est convexe car les
, alors il est convexe car les 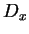 le sont et une intersection de convexes est convexe (c'est immédiat).
le sont et une intersection de convexes est convexe (c'est immédiat).
Réciproquement, supposons que
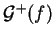 soit convexe. Le fait qu'il soit alors contenu dans l'intersection des
soit convexe. Le fait qu'il soit alors contenu dans l'intersection des 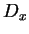 résulte de ce que le plan tangent à
résulte de ce que le plan tangent à
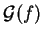 en
en 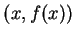 est l'unique hyperplan d'appui de
est l'unique hyperplan d'appui de
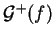 en ce point.
en ce point.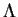
Lemme 68
Sous les hypothèses du Lemme
67,

est convexe si et seulement si
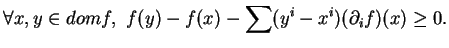 |
(7.1) |
Supposons d'abord que  soit convexe. Son épigraphe est alors l'intersection des
soit convexe. Son épigraphe est alors l'intersection des 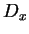 . Par conséquent, si
. Par conséquent, si
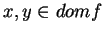 , comme
, comme
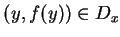 ,
Inversement, (18) montre que les points de la forme
,
Inversement, (18) montre que les points de la forme
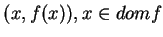 , sont dans l'intersection des
, sont dans l'intersection des 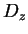 . Comme celle-ci est convexe, il en résulte que si
. Comme celle-ci est convexe, il en résulte que si
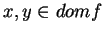 , alors le segment joignant
, alors le segment joignant 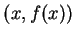 à
à 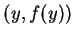 est contenu dans cette intersection, donc dans
est contenu dans cette intersection, donc dans
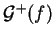 , c'est-à-dire
pour tout
, c'est-à-dire
pour tout ![$ t\in[0,1]$](img1714.gif) . Vu la Proposition 66,
. Vu la Proposition 66,  est donc convexe.
est donc convexe.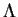




suivant: 7.3.3 Convexité & hessien
monter: 7.3 Fonctions convexes
précédent: 7.3.1 Inégalité de Jensen
Table des matières
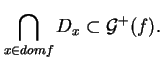
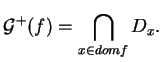
![]() est égal à l'intersection des
est égal à l'intersection des ![]() , alors il est convexe car les
, alors il est convexe car les ![]() le sont et une intersection de convexes est convexe (c'est immédiat).
le sont et une intersection de convexes est convexe (c'est immédiat).
![]() soit convexe. Le fait qu'il soit alors contenu dans l'intersection des
soit convexe. Le fait qu'il soit alors contenu dans l'intersection des ![]() résulte de ce que le plan tangent à
résulte de ce que le plan tangent à
![]() en
en ![]() est l'unique hyperplan d'appui de
est l'unique hyperplan d'appui de
![]() en ce point.
en ce point.![]()