2.3.2 Dimension

suivant: 2.3.3 Un exemple: les monter: 2.3 Variétés plongées précédent: 2.3.1 Définition Table des matières

2.3.2 Dimension

Les notations étant celles du Théorème 8, le Théorème 7 montre que le nombre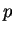

ne dépend pas du paramétrage choisi pour décrire

au voisinage de

. On appelle ce nombre la dimension de

. On le note 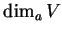$\dim_aV$ . Il est localement constant. En particulier, il est constant lorsque

est connexe et on le note alors $\dim V$ .

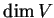Un espace topologique 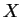est connexe s'il est "d'un seul tenant", ce qui, techniquement, se traduit par le fait que 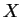n'admet pas de partition en deux ouverts. L'image continue d'un connexe est connexe: si 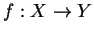$f:X\to Y$ est continu et si 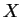est connexe, alors 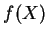est connexe pour la topologie induite par celle de 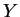. Cette propriété, facile à vérifier, est la version générale du théorème des valeurs intermédiaires. Les connexes de 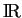$% latex2html id marker 17018 $ {\rm I\!R}$$ sont en effet les intervalles(^2.3). Dès lors, si $% latex2html id marker 17022 $ f:[a,b]\to {\rm I\!R}$$ est continu, est un intervalle. 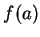Comme il contient et 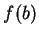, il contient aussi l'intervalle dont ils sont les extrémités.

Pour voir que 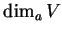$\dim_aV$ est constant lorsque est connexe, on observe que les ensembles

$% latex2html id marker 17034 $\displaystyle \big\{a\in V\vert\dim_aV=p\big\}, p\in{\rm I\!N}, $$

sont des ouverts disjoints dont l'union est . Il faut donc bien que l'un d'eux coïncide avec qui, sinon, ne serait pas connexe.

La codimension (en a) de

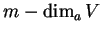est le nombre $m-\dim_aV$ . La dimension de

est le nombre de paramètres nécessaires pour décrire

au voisinage de

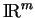tandis que sa codimension est le nombre d'équations cartésiennes qu'il faut imposer à un point de $% latex2html id marker 17052 $ {\rm I\!R}^m$$ pour qu'il appartienne à un voisinage de

dans

. Une hypersurface est une variété plongée de codimension

et une surface est une variété de dimension 2.

suivant: 2.3.3 Un exemple: les monter: 2.3 Variétés plongées précédent: 2.3.1 Définition Table des matières