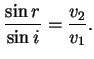suivant: 5.4 Espace tangent aux
monter: 5.3 Extrema liés: la
précédent: 5.3.2.2 Le quotient de
Table des matières
Nous supposons que la
lumière se déplace en minimisant le temps de parcours et que, de
plus, dans un milieux homogène,
sa vitesse est constante. Dans un tel milieu, ses trajectoires sont
donc des segments de droite(5.14). La question est de savoir comment est
modifiée sa trajectoire lorsqu'elle
traverse la surface  séparant deux milieux dans lesquels elle
circule à des vitesses différentes (lois de la réfraction) ou
lorsqu'elle se
réfléchit en un point de
séparant deux milieux dans lesquels elle
circule à des vitesses différentes (lois de la réfraction) ou
lorsqu'elle se
réfléchit en un point de  (lois de la réflexion). Dans le
premier cas, un rayon lumineux issu d'une source ponctuelle
(lois de la réflexion). Dans le
premier cas, un rayon lumineux issu d'une source ponctuelle 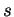 placée dans le premier milieu
traverse
placée dans le premier milieu
traverse  en
en  et poursuit sa trajectoire jusqu'en un point
cible
et poursuit sa trajectoire jusqu'en un point
cible 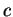 du second. Dans le second,
du second. Dans le second,  est le point en lequel le
rayon se réfléchit vers la
cible et celle-ci est dans le même milieu que la source. Nous
supposons que
est le point en lequel le
rayon se réfléchit vers la
cible et celle-ci est dans le même milieu que la source. Nous
supposons que  est une variété plongée (dans
est une variété plongée (dans
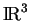 ) et
nous notons
) et
nous notons 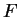 une
équation cartésienne la définissant dans un voisinage du point
d'incidence
une
équation cartésienne la définissant dans un voisinage du point
d'incidence  .
.
Dans l'un et l'autre des cas, le temps mis pour joindre 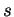 et
et 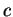 via un point
via un point
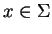 est
est
où 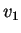 est la vitesse de la lumière avant l'incidence et
est la vitesse de la lumière avant l'incidence et 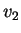 après (on a donc
après (on a donc 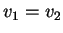 en cas de réflexion).
Par hypothèse,
en cas de réflexion).
Par hypothèse, 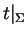 est stationnaire en
est stationnaire en  . par conséquent,
d'après la règle des multiplicateurs de Lagrange, il existe un nombre
. par conséquent,
d'après la règle des multiplicateurs de Lagrange, il existe un nombre
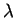 tels que
Ceci s'écrit
Comme
tels que
Ceci s'écrit
Comme
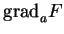 est la direction normale au plan tangent de
est la direction normale au plan tangent de  en
en  , nous en déduisons la première loi:
, nous en déduisons la première loi:
Le rayon incident (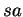 ), le rayon réfracté (ou réfléchi,
), le rayon réfracté (ou réfléchi, 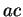 )
et la normale au point d'incidence à la surface de séparation (au
miroir,
)
et la normale au point d'incidence à la surface de séparation (au
miroir,  ) sont dans
un même plan.
) sont dans
un même plan.
Ce plan coupe le plan tangent à la surface  selon une droite.
En projettant scalairement l'égalité précédente sur le vecteur unité
normé
selon une droite.
En projettant scalairement l'égalité précédente sur le vecteur unité
normé 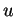 de celle-ci
orienté dans le sens de déplacement de la lumière, on obtient la
seconde loi:
de celle-ci
orienté dans le sens de déplacement de la lumière, on obtient la
seconde loi:
Les angles d'incidence et de réflexion sont égaux tandis que les
sinus des angles de réfraction et d'incidence sont dans le rapport
des vitesses de propagation dans les milieux successivement
traversés:
(Les angles d'incidence, etc. sont ceux que font les rayons
correspondants avec la normale de  au point d'incidence.)
au point d'incidence.)




suivant: 5.4 Espace tangent aux
monter: 5.3 Extrema liés: la
précédent: 5.3.2.2 Le quotient de
Table des matières
![]() et
et ![]() via un point
via un point
![]() est
est
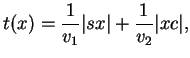
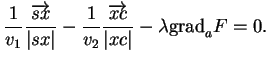
![]() ), le rayon réfracté (ou réfléchi,
), le rayon réfracté (ou réfléchi, ![]() )
et la normale au point d'incidence à la surface de séparation (au
miroir,
)
et la normale au point d'incidence à la surface de séparation (au
miroir, ![]() ) sont dans
un même plan.
) sont dans
un même plan.
![]() selon une droite.
En projettant scalairement l'égalité précédente sur le vecteur unité
normé
selon une droite.
En projettant scalairement l'égalité précédente sur le vecteur unité
normé ![]() de celle-ci
orienté dans le sens de déplacement de la lumière, on obtient la
seconde loi:
de celle-ci
orienté dans le sens de déplacement de la lumière, on obtient la
seconde loi: