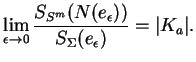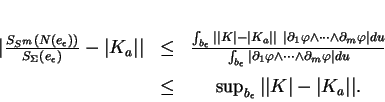suivant: 6.2.4.1 Courbure de Gauss
monter: 6.2 La seconde forme
précédent: 6.2.3 Le théorème de
Table des matières
Les valeurs propres de 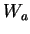 sont les
courbures principales et ses vecteurs propres, les directions principales,
de
sont les
courbures principales et ses vecteurs propres, les directions principales,
de  (en
(en  ). Le déterminant
). Le déterminant 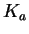 de
de 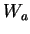 est sa courbure de Gauss.
est sa courbure de Gauss.
Il se fait qu'une hypersurface est déterminée à isométrie près par sa
première forme fondamentale et sa courbure de Gauss. Lorsque la
dimension de l'hypersurface
est paire, même cette dernière est déterminée par la première forme
fondamentale. C'est un théorème difficile que nous n'établirons pas
(6.14).
Voici une formule qui nous sera utile ultérieurement et dans laquelle
on voit intervenir la courbure de Gauss dans les dérivées de 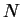 .
.
Proposition 51
Les
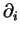
représentant les dérivées par rapport aux paramètres
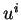
,
Notons 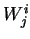 les composantes de la matrice représentant
les composantes de la matrice représentant 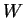 dans la base de l'espace tangent formée par les
dans la base de l'espace tangent formée par les
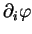 .
On a
Par conséquent, si l'on tient compte de l'antisymétrie du produit
vectoriel comme on l'a déjà fait plus haut à l'occasion du changement
de paramétrage dans
l'élément de surface,
.
On a
Par conséquent, si l'on tient compte de l'antisymétrie du produit
vectoriel comme on l'a déjà fait plus haut à l'occasion du changement
de paramétrage dans
l'élément de surface,
Corollaire 52
Si
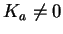
alors
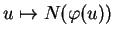
est un paramétrage de la sphère
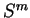
au voisinage de
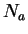
.
En effet, si 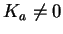 , alors la différentielle de
, alors la différentielle de
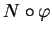 est injective en
est injective en
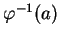 . La propriété résulte alors d'un théorème d'analyse non linéaire.
. La propriété résulte alors d'un théorème d'analyse non linéaire.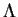
Ainsi, si 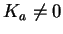 , lorsque
, lorsque
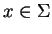 décrit un voisinage de
décrit un voisinage de  , l'application de Gauss le transforme en un voisinage de
, l'application de Gauss le transforme en un voisinage de 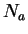 dans la sphère
dans la sphère 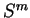 . Les ``surfaces'' des voisinages en question sont dans un rapport lié à la courbure de Gauss.
. Les ``surfaces'' des voisinages en question sont dans un rapport lié à la courbure de Gauss.
Proposition 53
Supposons que
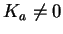
. Notons respectivement
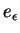
et
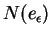
les images par

et
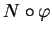
de la boule
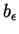
de centre
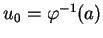
et de rayon
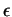
de
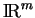
, où
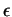
est assez petit pour que cette boule soit contenue dans
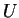
. On a
En effet, d'après la proposition ci-dessus,
Puisque 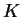 est continu, cette dernière expression peut être rendue aussi petite que l'on veut.
est continu, cette dernière expression peut être rendue aussi petite que l'on veut.
Sous-sections




suivant: 6.2.4.1 Courbure de Gauss
monter: 6.2 La seconde forme
précédent: 6.2.3 Le théorème de
Table des matières
![]() .
.
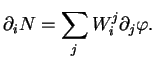
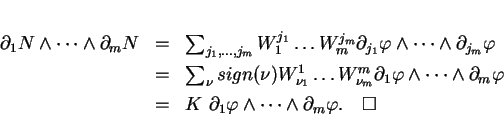
![]() , lorsque
, lorsque
![]() décrit un voisinage de
décrit un voisinage de ![]() , l'application de Gauss le transforme en un voisinage de
, l'application de Gauss le transforme en un voisinage de ![]() dans la sphère
dans la sphère ![]() . Les ``surfaces'' des voisinages en question sont dans un rapport lié à la courbure de Gauss.
. Les ``surfaces'' des voisinages en question sont dans un rapport lié à la courbure de Gauss.