



suivant: 5.4.1.1 L'hyperboloïde à une
monter: 5.4 Espace tangent aux
précédent: 5.4 Espace tangent aux
Table des matières
Une surface réglée  est l'image
est l'image
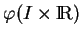 d'une fonction de classe
d'une fonction de classe 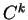 de la forme
de la forme
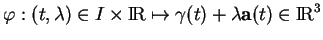 |
|
|
(5.2) |
où
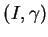 est un paramétrage d'un arc régulier de courbe
est un paramétrage d'un arc régulier de courbe 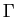 et
et
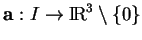 .
On suppose de plus que
.
On suppose de plus que
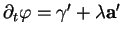 et
et
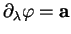 sont toujours
linéairement indépendants.
Une surface réglée est donc formée de droites, les génératrices, qui s'appuient sur une directrice
sont toujours
linéairement indépendants.
Une surface réglée est donc formée de droites, les génératrices, qui s'appuient sur une directrice 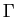 .
.
L'ensemble  n'est pas toujours une surface au sens de la définition donnée plus haut car l'application
n'est pas toujours une surface au sens de la définition donnée plus haut car l'application  n'est pas nécessairement
injective comme le veut la définition d'un paramétrage. A cause de l'hypothèse sur ses dérivées partielles, elle est cependant injective quand on la restreint à
un voisinage suffisamment petit de chaque point
n'est pas nécessairement
injective comme le veut la définition d'un paramétrage. A cause de l'hypothèse sur ses dérivées partielles, elle est cependant injective quand on la restreint à
un voisinage suffisamment petit de chaque point
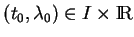 (5.15). Il est donc légitime de dire que le plan
(5.15). Il est donc légitime de dire que le plan
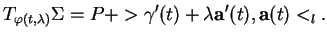 |
(5.3) |
est tangent à  en
en
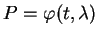 . Comme pour les tangentes aux arcs de courbes, il peut donc y avoir plusieurs plans tangents à
. Comme pour les tangentes aux arcs de courbes, il peut donc y avoir plusieurs plans tangents à  en un
même point.
en un
même point.
Sous-sections




suivant: 5.4.1.1 L'hyperboloïde à une
monter: 5.4 Espace tangent aux
précédent: 5.4 Espace tangent aux
Table des matières
![]() n'est pas toujours une surface au sens de la définition donnée plus haut car l'application
n'est pas toujours une surface au sens de la définition donnée plus haut car l'application ![]() n'est pas nécessairement
injective comme le veut la définition d'un paramétrage. A cause de l'hypothèse sur ses dérivées partielles, elle est cependant injective quand on la restreint à
un voisinage suffisamment petit de chaque point
n'est pas nécessairement
injective comme le veut la définition d'un paramétrage. A cause de l'hypothèse sur ses dérivées partielles, elle est cependant injective quand on la restreint à
un voisinage suffisamment petit de chaque point
![]() (5.15). Il est donc légitime de dire que le plan
(5.15). Il est donc légitime de dire que le plan