



suivant: 4 Quelques cas particuliers
monter: 3.2 Groupes de matrices
précédent: 3.2.6 Le groupe affine
Table des matières
Comme espace vectoriel sur
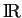 , l'ensemble
, l'ensemble
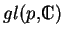 des matrices carrées, de dimension
des matrices carrées, de dimension
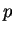 , dont les coefficients
sont complexes est isomorphe à
, dont les coefficients
sont complexes est isomorphe à
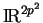 . Le groupe
. Le groupe
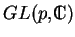 des éléments non singuliers de
des éléments non singuliers de
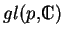 en est un ouvert. On y
distingue différents
sous-groupes, analogues complexes des exemples précédents. Ce sont
des variétés plongées dans
en est un ouvert. On y
distingue différents
sous-groupes, analogues complexes des exemples précédents. Ce sont
des variétés plongées dans
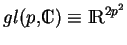 . (Les
vérifications sont laissées à
titre d'exercices, ainsi que le calcul des dimensions.) Outre
. (Les
vérifications sont laissées à
titre d'exercices, ainsi que le calcul des dimensions.) Outre
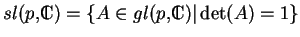 , il y a le groupe unitaire
, il y a le groupe unitaire
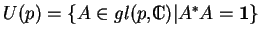 et son sous-groupe
et son sous-groupe
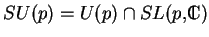 (3.6).
(3.6).